Capítulo 6 Intervalos de Confianza mediante bootstrap

6.1 Inicio

En esta sección analizaremos más a fondo una técnica (llamada bootstrap) para realizar intervalos de confianza. Comenzaremos haciéndolo para el caso de experimentos y luego veremos cómo es distinto para el caso de muestreo aleatorio en poblaciones finitas y realizaremos ese caso.

6.2 Intervalos asintóticos

Los intervalos de confianza que hemos construido hasta ahora son con la idea de normalidad asintótica; se basan en la idea de que:

\[ Z =\lim_{N-n, n \to \infty} \sqrt{\frac{1}{\textrm{Var}(\bar{x}_{\mathcal{S}})}} \cdot \Big( \frac{1}{n}\sum_{i = 1}^N x_i \mathbb{I}_{\mathcal{S}}(x_i) - \bar{x}_{\mathcal{U}}\Big) \sim \text{Normal}(0,1) \]

Es decir, si tuviéramos una población infinita \(N\) y una muestra infinita \(n\) entonces la diferencia entre la media muestral y la media verdadera (normalizadas por la varianza) tienen una distribución normal. Empero, esto no siempre funciona como el siguiente con \(n = 15\) muestras nos enseña:

#Tomar muestras de tamaño pequeño
n       <- 15
lambda  <- 0.1
Z       <- qnorm(0.975)
nsim    <- 100    #Cantidad sims
N       <- 1000000 #Tamaño poblaciím
pop     <- sample(c(0,1), N, replace = TRUE, prob = c(1 - lambda, lambda))


#Creamos las bases donde guardar los datos
datos <- data.frame(matrix(NA, ncol = 3, nrow = nsim))
colnames(datos) <- c("IC_Bajo","Media","IC_Alto")
datos$Sim       <- 1:nsim

#Obtenemos 100 muestras
for (i in 1:nsim){
  muestra        <- sample(pop, n)
  datos$Media[i] <- mean(muestra)
  varianza       <- (1 - n/N)/n*var(muestra)
  datos$IC_Bajo[i]  <- datos$Media[i] - Z*sqrt(varianza)
  datos$IC_Alto[i]  <- datos$Media[i] + Z*sqrt(varianza)
}

ggplot(datos, aes(x = Sim)) +
  geom_errorbar(aes(ymin = IC_Bajo, ymax = IC_Alto)) +
  geom_point(aes(y = Media), color = "red") +
  geom_hline(aes(yintercept = mean(pop) )) +
  theme_bw() +
  labs(
    x = "Simulación",
    y = "Proporción p",
    title = "Estimación de p para una Bernoulli"
  )

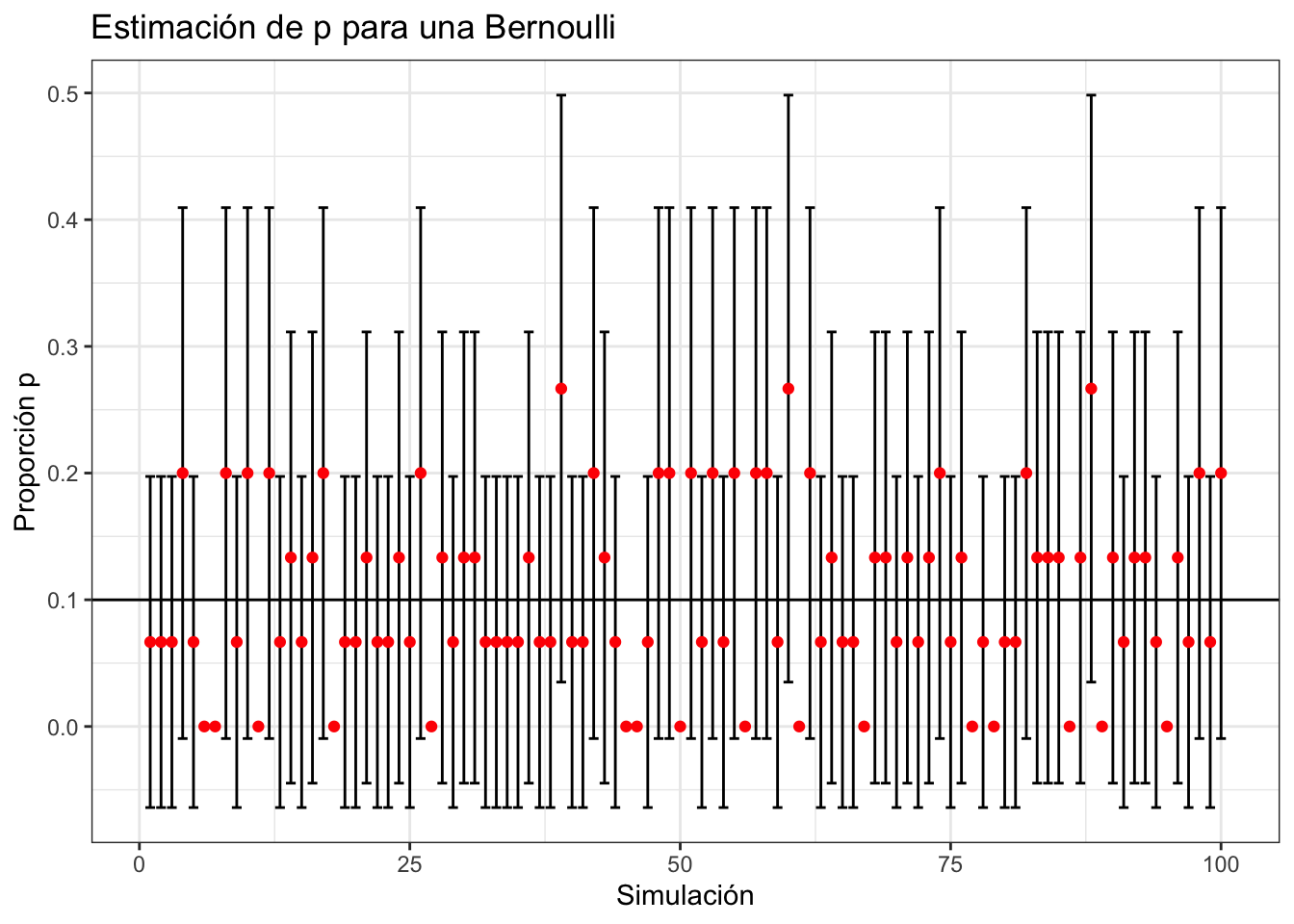En el caso de la Bernoulli, por ejemplo, se puede un mejor intervalo de confianza para cuando la proporción \(\hat{p} = 0\) bajo una hipótesis distribucional. Esta se encuentra en el paquete binom de R:

library(binom)
binom.confint(0, n, conf.level = 0.95, method = 'exact')
##   method x  n mean lower     upper
## 1  exact 0 15    0     0 0.2180194

La deducción de dichos intervalos se hace a través de un esquema distinto de muestreo: muestreo basado en modelos.

6.3 Muestreo basado en modelos

Quizá en otras clases de estadística viste muestreo de otra manera. Lo usual en Estadística Matemática es suponer se tienen un conjunto de \(n\) variables aleatorias independientes idénticamente distribuidas que representan la cantidad de interés \(\{ Y_1, Y_2, \dots, Y_n\}\). De dichas variables se observa que toman los valores \(\{y_1, y_2, \dots, y_n\}\) que son los medidos en la muestra. Aquí no se considera que haya un conjunto finito (universal) dado por la población sino que todas las variables provienen de una metapoblación (universo infinito de posibilidades). Así, por ejemplo, las alturas de individuos podrían tener una distribución gamma truncada y las alturas de personas en particular corresponden a realizaciones independientes de dichas \(Y_i\). Este enfoque lo que hace es convertir el problema de estimación en un problema de predicción. No es que la altura de un individuo sea aleatoria en el sentido de que siempre cambie sino que por nuestra ignorancia nosotros modelamos dicha altura con una variable aleatoria que representa, en esta metapoblación la altura de una cantidad infinita de individuos posibles. Bajo este esquema, una muestra aleatoria está dada por: \[ \mathcal{Y}_{(n)} = \{ Y_1, Y_2, \dots, Y_n\} \] y la muestra observada es:

\[ \mathcal{y}_{(n)} = \{ y_1, y_2, \dots, y_m\} \] Donde suponemos que lo que se observó fue que \(Y_i = y_i\). Un punto relevante aquí es que como las \(\{Y_i\}\) son variables aleatorias éstas siguen algún modelo. En particular, se eligen modelos paramétricos para estos casos en los que la distribución asintótica no funciona. El problema de estimación se convierte ya sea en estimar el parámetro de la función de densidad (por ejemplo el \(\Theta = (\mu,\sigma)^T\) de la normal o el \(\lambda\) de una Poisson) o una función del mismo (como puede ser la mismísima función de densidad o distribución acumulada).

Nota El enfoque basado en modelos es muy bueno cuando se tienen pocos dados (o mal medidos) y las observaciones por sí mismas no son suficientes para poder generar información. En ese caso se hacen hipótesis adicionales (como un modelo) para los procesos de estimación.

Veamos un ejemplo de generación de intervalos para la media (\(\lambda\)) de una variable Poisson.

6.3.1 Ejemplo Poisson

Consideremos una muestra aleatoria \(\mathcal{Y}_{(n)} = \{ Y_1, Y_2, \dots, Y_n\}\) de variables que se distribuyen \(\text{Poisson}(\lambda)\). Sabemos de proba (y si no lo sabemos no te apures, este ejemplo es sólo para ilustrar, no vamos a hacer más de esto) que la suma de variables aleatorias Poisson es Poisson, de donde: \[ \sum\limits_{i = 1}^n Y_i \sim\text{Poisson}(n \cdot \lambda) \] por lo cual: \[ n \bar{Y} = \sum\limits_{i = 1}^n Y_i \sim\text{Poisson}(n\lambda) \] tenemos entonces que \(\mathbb{E}[\bar{Y}] = \lambda\) (es insesgado). En este caso tomaremos que en particular observamos \[ \hat{y} = n \bar{y} = \sum\limits_{i = 1}^n y_i \]

Observamos que para \(y\) fijo, la distribución Poisson es decreciente antes de la media en \(\lambda\) y creciente después de la media:

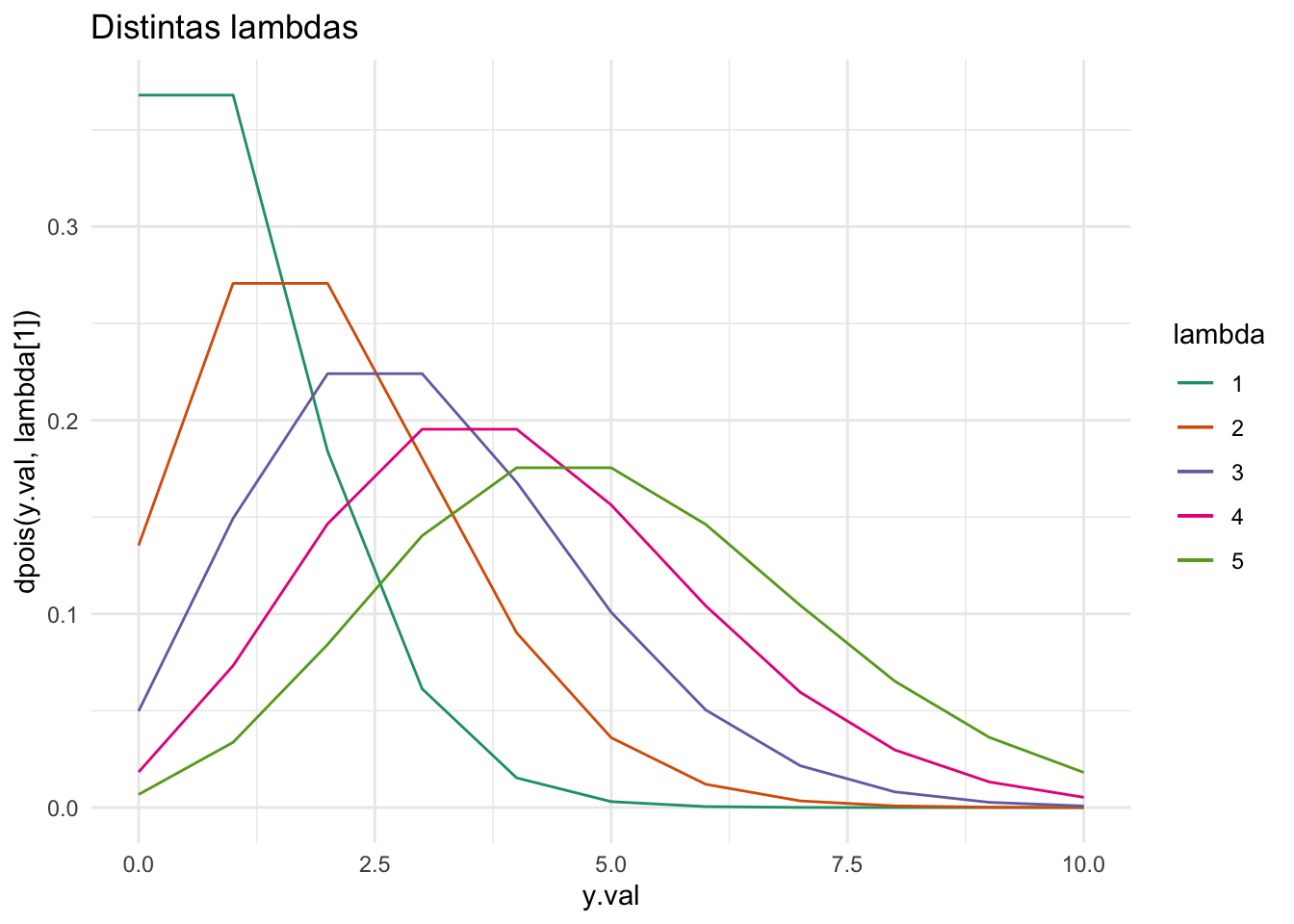
Podemos entonces obtener un estimador \(\lambda\) consideramos los valores \(\lambda_1\) y \(\lambda_2\) tales que: \[ \sum\limits_{k \leq \hat{y}} \dfrac{(n\lambda_1)^{\hat{y}} e^{-n\lambda_1}}{\hat{y}!} = \alpha / 2 \quad \text{ y } \quad \sum\limits_{k \geq \hat{y}} \dfrac{(n\lambda_2)^{\hat{y}} e^{-n\lambda_2}}{\hat{y}!} =\alpha / 2 \]

El cual podemos encontrar facilmente con ayuda de R:

#Obtenemos la muestra
n         <- 20
ybarra    <- sum(rpois(n, 1/5))
alpha.val <- 0.05

#Optimizamos
func.opt.1 <- function(lambda){ppois(ybarra, n*lambda) - alpha.val/2}
lambda.1   <- uniroot(func.opt.1, lower = 0, upper = 10, tol = 1.e-10)$root

func.opt.2 <- function(lambda){1 - ppois(ybarra, n*lambda) + dpois(ybarra, n*lambda) - alpha.val/2}
lambda.2   <- uniroot(func.opt.2, lower = 0, upper = 10, tol = 1.e-10)$root

c("Lower" = lambda.2, "Upper" = lambda.1)
##      Lower      Upper 
## 0.03093361 0.43836365

Nota Estos intervalos se conocen como fiduciarios/fiduciales. La idea es obtener los valores de \(\lambda\) tales que \(\bar{Y} = Y\) con un intervalo de probabilidad \((1 - \alpha)\times 100 \%\).

En nuestro caso para análisis de encuestas no podemos usar directamente los resultados de estadística matemática que refieren más a experimentos pues en ello se supone independencia (lo cual casi nunca es cierto para encuestas). Sin embargo, tras el modelo que hemos estudiado ahora sí podríamos generar variables tipo las de estadística matemática con una hipótesis distribucional dadas por \(\{Z_i\}\) donde \[ Z_k = \mathbb{I}(x_k) \] pero sin que \(Z_i\) sea independiente de \(Z_j\). En este caso las \(Z_i\) siguen una distribución multivariada dictada por las \(\pi_k\).

6.3.2 Ejercicio

Obtén los intervalos fiduciarios para una variable aleatoria Bernoulli. Considera que la muestra está dada por:

set.seed(646)
muestra <- sample(c(0,1), 13, replace = TRUE, prob = c(0.2, 0.8))

Recuerda Si \(X_i \sim \textrm{Bernoulli}(p)\) entonces \(\sum_{i = 1}^n X_i \sim \textrm{Binomial}(n,p)\).

6.4 Intervalos Bootstrap

Los intervalos anteriores requieren de manera implícita de la función de distribución acumulada original la cual puede ser muy complicada o desconocida. Los intervalos Bootstrap buscan aproximar dicha función mediante un remuestreo. La demostración exacta (con medida) de por qué funciona el Boostrap la puedes ver en Asymptotic Statistics. La idea es reconstruir la función de distribución acumulada mediante remuestreo de la base (de una mejor manera aún que con la \(\hat{F}\) empírica) y calcular estadísticos a partir de ella. Algunos estadísticos que se pueden calcular a partir de ella es, por ejemplo, la media muestral o la varianza así como los cuantiles. Para ello definiremos un concepto importante:

Definición Un estadístico \(t\) es un funcional estadístico si \(t\) es simétrica para \(y_1, y_2, \dots, y_N\). Dicho de otra forma, \(t\) depende solamente de los valores ordenados \(y_{(1)}, y_{(2)}, \dots, y_{(N)}\) y no del orden preciso (de la muestra o la población). En este caso \(t\) depende sólo de la función de distribución y se escribe como \(t(F)\) (en el caso poblacional) ó \(t(\hat{F})\) en el caso muestral.

Un ejemplo de estadístico es la media pues (suponiendo \(F\) discreta) por ejemplo: \[ \mu = \sum\limits_x x\big[\underbrace{F(x) - F(x^-)}_{\mathbb{P}(X = x)}\big] \] Mientras que de manera muestral la estimación es idéntica mediante estimadores: \[ \hat{\mu} = \sum\limits_x x\big[\underbrace{\hat{F}(x) - \hat{F}(x^-)}_{\hat{\mathbb{P}}(X = x)}\big] \] donde la notación \(F(x^-) = \lim_{y \to x^-} F(y)\).

Un ejemplo adicional es la mediana que corresponde a: \[ \textrm{Mediana} = F^{-1}(1/2) \] donde \[ F^{-1}(p) = \inf \{ x \in \mathbb{R} : F(x) \geq p\} \] es una pseudoinversa conocida como la función cuantil. (En el caso de \(F\) continua es una inversa “bien” pero discreta no lo es porque esa cosa ni es invertible).

La idea de Bootstrap (con una demostración bastante técnica) es que para una \(\hat{F}_B\) función de distribución empírica acumulada generada por Boostrap se tiene que: \[ \sqrt{n} \big( t(\hat{F}_{\text{B}}) - t(\hat{F}))) \] converge en distribución al mismo límite que: \[ \sqrt{n} \big( t(\hat{F}) - t(F))) \] para cualquier \(t\) función Hadamard-diferenciable..

Lo que en humano quiere decir es que muchísimos funcionales estadísticos convergen al verdadero. Lo interesante de Bootstrap (usualmente) no va a ser estimar el \(t\) sino estimar un intervalo para \(t\) a partir de remuestrear varias \(\hat{F}\) mediante simulación.

Nota que no sé dónde poner Un tipo de Bootstrap específico es el Jacknife donde se elimina aleatoriamente un elemento de la base. Model Assisted Survey Sampling lo pone como otra cosa pero en realidad es un boostrap bajo otro método.

6.4.1 Boostrap bajo un modelo

Regresemos a nuestro ejemplo Poisson de la media pero esta vez usando Boostrap. Para ello consideramos la muestra de tamaño \(n = 20\).

n         <- 20
muestra   <- rpois(n, 1/5)
alpha.val <- 0.05
nsim      <- 1000 #Mil simulaciones nada más para no trabar
media.completa <- mean(muestra)
media     <- rep(NA, nsim)
for (i in 1:nsim){
  remuestreo <- sample(muestra, n, replace = TRUE)
  media[i]   <- mean(remuestreo)
}

#Cálculo de cotas
lado.sup <- quantile(media - media.completa, alpha.val/2)
lado.inf <- quantile(media - media.completa, 1 - alpha.val/2) 

print(paste0("El intervalo es [", media.completa - lado.inf, 
             ",", media.completa - lado.sup,"]"))
## [1] "El intervalo es [-0.05,0.4]"

El algoritmo es como sigue: 1. Obtén una muestra aleatoria simple con reemplazo \(X_1^B, X_2^B, \dots, X_n^B \sim \hat{F}\) y calcula \(t(X_1^B, X_2^B, \dots, X_n^B)\) 2. Repite \(n\) veces (este \(n\) se decide de recalculando la \(n\) como si viniera de una muestra para tener la precisión deseada) o bien por convergencia. 3. Calcula los cuantiles simulados correspondientes \(\delta_1 = (t_B - t)_{\alpha/2}\) y \(\delta_2 = (t_B - t)_{1 - \alpha/2}\) 4. El intervalo es \(t - \delta_1\) y \(t - \delta_2\)

Nota Boostrap no es perfecto para todo. Por ejemplo si se tiene una muestra de variables aleatorias \(X_i \sim \text{Unif}(0,1)\) y se busca \(t_n = \min \{ X_i \}\) bajo Bootstrap se puede demostrar que \[ n t_n \to \text{Exponencial}(1) \] lo cual no corresponde al valor verdadero

6.4.2 Boostrap de una muestra

En el caso de una muestra aleatoria simple ponderada con estratos excluyentes \(S_1, S_2, \dots, S_{H}\) de tamaños \(N_1, N_2, \dots, N_H\) para cada estrato \(S_h\) seleccionamos una muestra bootstrap a partir de lo cual podemos calcular una función de distribución empírica para cada estrato \(\hat{F}_h\) y repetir el algoritmo (para cada estrato):

  1. Crea una subpoblación \(U^f_h\) fija de tamaño \(k = \Big\lfloor \frac{N_h}{n_h} \Big\rfloor\) repitiendo la original \(k\) veces.
  2. Obtén \(U^c_h\) una muestra aleatoria de \(S_h\) de tamaño \(N - nk\). Crea la pseudo población bootstrap como \(U^{boot}_h = U^c_h \cup U^f_h\).
  3. Obtén una muestra de \(U^{boot}_h\) de tamaño \(n_h\) y recalcula el parámetro de interés \(t_B = t(F_h^{boot})\).
  4. Repite \(m\) veces (este \(m\) se decide de recalculando la \(n\) como si viniera de una muestra para tener la precisión deseada) o bien por convergencia.
  5. Calcula los cuantiles simulados correspondientes \(\delta_1 = (t_B - t)_{\alpha/2}\) y \(\delta_2 = (t_B - t)_{1 - \alpha/2}\)
  6. El intervalo es \(t - \delta_1\) y \(t - \delta_2\)

El método anterior es el desarrollado por Booth, Butler y Hall; sin embargo no es el único que existe. Para poblaciones finitas te sugiero checar el compendio de Mashreghi, Haziza y Léger donde vienen varios métodos.

6.4.3 Ejemplo

Calcular la mediana de la siguiente población:

pop.total <- c(rnorm(100), rexp(100), rpois(100, 2))
N <- length(pop.total)

#Verdadera mediana
mediana.real <- median(pop.total)

#Obtenemos muestra de tamaño n = 25 por ejemplo
n <- 25
muestra          <- sample(pop.total, 25)
mediana.muestral <- median(muestra)
mediana          <- rep(NA, nsim)

print(paste0("El valor real es ", mediana.real))
## [1] "El valor real es 0.629704617234562"
#Tamaño de bootstrap
k.val <- floor(N/n)
Uf    <- rep(muestra, k.val)


for (i in 1:nsim){
  Uc         <- sample(muestra, N - n*k.val, replace = TRUE)
  Uboot      <- c(Uf, Uc)
  remuestreo <- sample(Uboot, n, replace = FALSE)
  mediana[i] <- median(remuestreo)
}

#Cálculo de cotas
lado.sup <- quantile(mediana - mediana.muestral, alpha.val/2)
lado.inf <- quantile(mediana - mediana.muestral, 1 - alpha.val/2) 

print(paste0("El intervalo es [", mediana.muestral - lado.inf, 
             ",", mediana.muestral - lado.sup,"]"))
## [1] "El intervalo es [-0.12970966652169,0.838248776470654]"

6.4.4 Ejercicio

De una población de árboles se midieron las alturas según distintos tipos de semilla. Esta información está contenida en R en una base de datos precargada:

data(Loblolly)
arboles <- Loblolly

  1. Suponiendo que para la semilla \(305\) se realizó muestreo aleatorio simple sin reemplazo de un total \(N = 100\) árboles, estima la mediana de altura y los cuantiles \(0.25\) y \(0.75\) de la misma junto con sus intervalos de confianza mediante bootstrap.

  2. Suponiendo que para la semilla \(307\) se realizó muestreo aleatorio simple sin reemplazo de un total \(N = 300\) árboles, estima la media y varianza de altura junto con sus intervalos de confianza mediante bootstrap.

  3. Estima para todos los árboles (es decir no sólo para los estratos sino para la población completa) la altura promedio, la altura mediana, los cuantiles \(0.25\) y \(0.75\) de altura así como la curtosis y la asimetría de la misma junto con sus intervalos de confianza mediante bootstrap suponiendo las \(N_h\) son:

Semilla Nh
301 960
303 1008
305 968
307 1029
309 995
311 994
315 1025
319 979
321 1008
323 1046
325 1064
327 1012
329 996
331 1015
  1. Considera una población de tamaño \(N = 1000\) y una muestra aleatoria sin reemplazo de la misma de tamaño \(n = 71\) dada por:
set.seed(64)
muestra <- rlnorm(71)

grafica la función de distribución empírica (asociada a la muestra) y grafica intervalos de confianza para la misma en el intervalo \([0.1, 0.9]\).

Tip Genera intervalos de confianza mediante boostrap asociados a \(\hat{F}(0.1)\), \(\hat{F}(0.2)\), \(\hat{F}(0.3)\), \(\hat{F}(0.4)\), \(\hat{F}(0.5)\), \(\hat{F}(0.6)\), \(\hat{F}(0.7)\), \(\hat{F}(0.8)\), y \(\hat{F}(0.9)\)