Capítulo 2 Conceptos

Este libro trata sobre datos y encuestas que estudian poblaciones a través de muestras. Antes de empezar con las matemáticas es necesario definir estos conceptos para tener claro de qué se habla. El más importante es la distinción entre encuesta y experimento: todo este libro hablará sobre encuestas, dejando la estadística para experimentos para otras notas.

Experimento Cualquier diseño de estudio donde la investigadora puede, potencialmente, replicar cuantas veces desee el estudio y obtener cuantas mediciones sean necesarias. El objeto de estudio NO es una población finita. Por ejemplo: alimentar ratones con una sustancia y medir su presión arterial (pueden obtenerse cuantos ratones sean necesarios), determinar la vida media de un compuesto (puede hacerse cuantos kilogramos de la sustancia se requieran) o establecer si una forma de enseñanza de estadística genera mejores resultados en los exámenes que otra (se pueden obtener tantos alumnos como se desee y enseñarles de X o Y forma hasta distinguir una diferencia si es que hay).

Nota Si has escuchado hablar de inferencia estadística usualmente esto es lo que se enseña cuando se consideran variables aleatorias independientes idénticamente distribuidas. Muchos de los teoremas (como normalidad aproximada) funcionan cuando el tamaño de tu muestra, \(n\), tiende a infinito, \(n \to \infty\). Eso funciona súper bien cuando lo que se analiza son experimentos que se pueden repetir tantas veces como sea necesario para obtener la aproximación límite. Este libro no trata sobre experimentos sino sobre encuestas y en una encuesta usualmente se considera una población finita por lo que no se pueden obtener infinitas mediciones.

Encuesta Una encuesta es un diseño de estudio donde se busca determinar el estado actual o una característica de una población finita (tamaño usualmente denotado \(N\)). Una encuesta no es replicable en igualdad de condiciones y está sujeta a que, a lo más, puede obtener tantas mediciones como el tamaño de la población. Por ejemplo: realizar un cuestionario sobre salud mental dentro de la población de estudiantes (no es replicable porque si se vuelve a hacer, la salud mental de los estudiantes o la población ya cambió); determinar el tamaño en bytes del Internet (la población es finita); medir la altura de los árboles de un bosque (finito y no replicable).

Nota Una encuesta no es un cuestionario. Algunas encuestas de salud, por ejemplo, toma muestras de sangre de las personas para determinar la proporción de personas con diabetes. Esta encuesta no es un cuestionario (no tiene una pregunta) pero sí es una encuesta (busca determinar el estado actual o una característica de una población finita). Lo mismo ocurre cuando se busca determinar la cantidad de árboles en un bosque (no se les pregunta a los árboles cuántos son) o cuando se quiere establecer el peso promedio de las vacas en distintos centros ganaderos (no se les pregunta a las vacas cuánto pesan).

No todas las encuestas tienen sentido como cuestionarios

Población Cualquier conjunto no vacío. Algunos ejemplos de poblaciones incluyen: las personas que viven en Guatemala (si me interesa saber algo de los guatemaltecos en general), los árboles del Amazonas (si quiero saber cosas de ecología en torno al río), los perros callejeros en Ciudad de México, los consumidores de una marca de cereal, los coches que transitan por Dubai o los granos de arena en una playa específica de Cancún.

Nota: Las poblaciones no necesariamente son de seres vivos son sólo conjuntos de cosas que se están estudiando. Las poblaciones usualmente están restringidas al tiempo y al espacio por lo que es importante tener una definición clara de quiénes sí están en el estudio, quiénes no y por qué.

Nota: En la mayoría de los problemas de encuestas que enfrentaremos suponemos que la población es de tamaño finito \(N\). Esto en contraste con un experimento donde la población es de tamaño infinito.

Población objetivo El conjunto de elementos que formarán parte del estudio. Definir la población objetivo es complicado en algunas situaciones; por ejemplo, si se desea saber si los mexicanos están a favor o en contra de legalizar la marihuana hay que establecer quiénes son los mexicanos. ¿Cuentan las personas con nacionalidad mexicana que residen en el extranjero? ¿Cuentan los menores de edad? ¿Qué pasa con los extranjeros que son residentes?
Población muestreada Es el conjunto de elementos sobre los cuales se tomó la muestra para el análisis estadístico. Idealmente la población objetivo y la muestreada deberían de ser igual pero el mundo no es tan bello. En encuestas de consumo, por ejemplo, usualmente no se muestrean zonas remotas o de muy bajos recursos. En encuestas de elecciones si bien la población objetivo son todas las personas que voten el día de la elección, como la mayoría se hacen antes de la elección (exceptuando las de salida) entonces se aproxima la definición de votante buscando incluir sólo aquellos que estén registrados en el padrón electoral o bien aquellos que al ser encuestados digan que sí van a votar.

A veces a la población se le conoce como el conjunto universo y es por esto que se denota: \[ \mathcal{U} = \{ u_1, u_2, \dots \} \] con \(u_i\) siendo sus elementos. Nosotros (hasta que se diga lo contrario) supondremos que la muestreada coincide con la objetivo y por tanto esa \(\mathcal{U}\) será sólo la población.

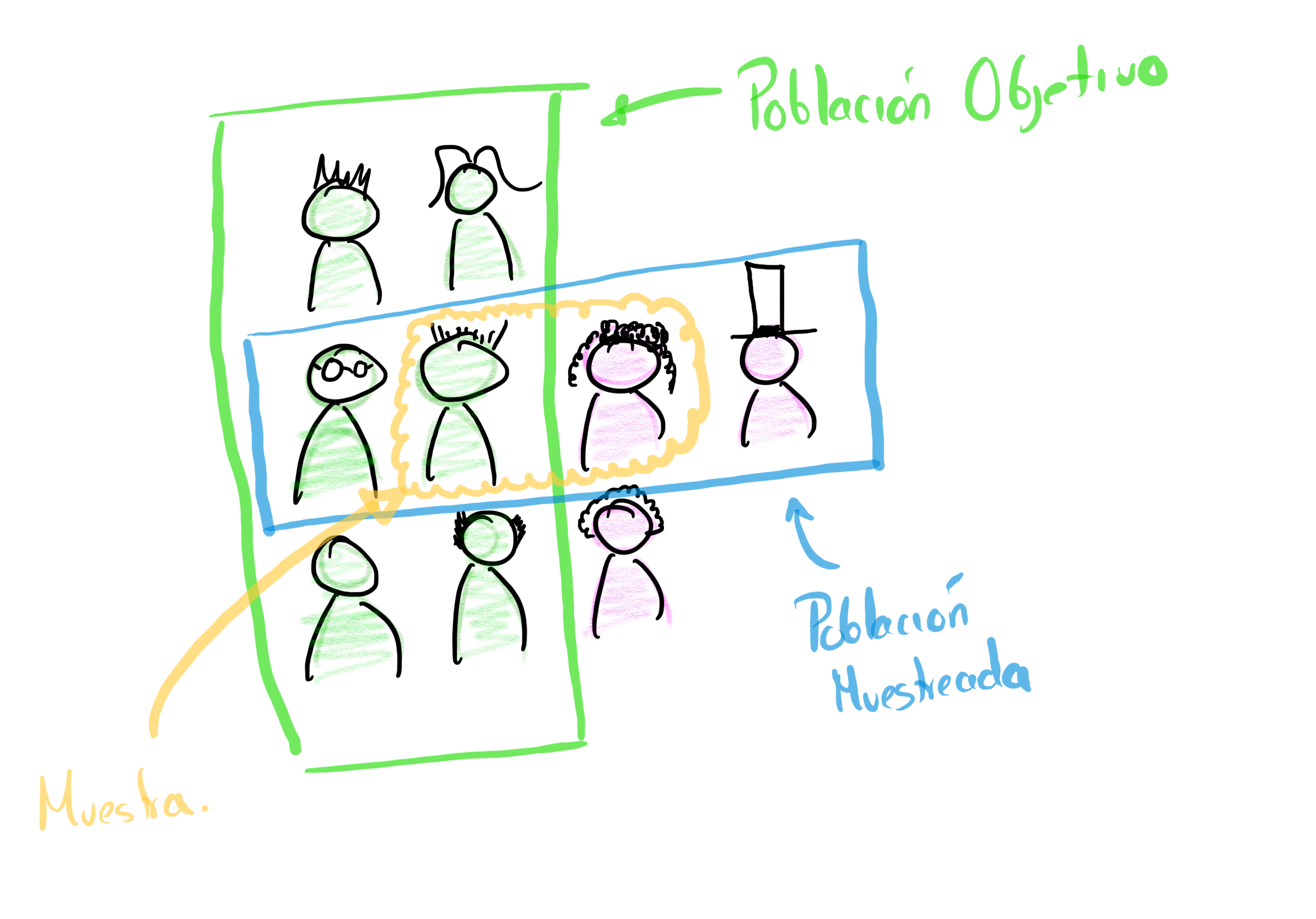
Diferencia entre población objetivo, población muestreada y muestra

Muestra Un subconjunto de la población muestreada. Si la muestra coincide con la población muestreada se dice que es un censo. Los “mejores” censos (para nosotros) son aquellos donde la población muestreada y la población objetivo coinciden (porque ya medimos todo lo que queríamos). Para el propósito de estas notas los únicos censos que consideraremos son aquellos donde la población muestreada es la objetivo.

La muestra es un subconjunto de la población: \[ \mathcal{S} = \{ s_1, s_2, \dots \} \subseteq \mathcal{U} \] con \(s_i\) siendo sus elementos. Nosotros sólo consideraremos muestras que son de tamaño finito, \(n\).

Nota: Hasta ahora no estamos hablando de muestras aleatorias. Esta definición habla de cualquier subconjunto no necesariamente uno que se haya obtenido por algún mecanismo aleatorio. Por ejemplo, si durante una pandemia se le pide a todas las personas de una población con apellidos de la A a la F acudan a una institución esto sí es una muestra (dado que es subconjunto de la población) pero podría argumentarse no es una muestra aleatoria (pues el proceso de selección fue determinista).

Nota A menos que se especifique lo contrario, el vació, \(\emptyset\) es una muestra.

Hay que ser muy claros para especificar que queremos una muestra con \(n >0\)

Marco muestral Una lista a partir de la cual se selecciona la muestra para la encuesta. Puede ser, en un salón de clases, la lista completa de alumnos. En estudios de agricultura usualmente la lista son parcelas de tierra aunque interese estudiar los cultivos mientras que en poblaciones grandes de personas el marco suele ser una lista de casas (dado que no se sabe qué persona vive dónde) o bien un mapa de calles y colonias. Para el INEGI es común usar las Áreas Geoestadísticas Básicas (AGEB) las cuales son divisiones fijas (pequeñísimas, como una manzana) del mapa de México.

Este marco muestral está amañado

Unidad de muestreo Una unidad que puede seleccionarse del marco muestral. Por ejemplo, en la lista de casas la unidad de muestreo sería una casa. Por otro lado, en una lista de parcelas la unidad es la parcela. Si se tiene una lista de estudiantes en un grupo la unidad serían los estudiantes. Puede que haya múltiples unidades de muestreo en la misma encuesta por ejemplo, si se desea hacer una encuesta para evaluar alumnos de las escuelas. Suponiendo que el muestreo ocurre de la siguiente forma: 1) primero sólo se tiene la lista de escuelas por lo que se seleccionan al azar un número de escuelas; 2) una vez las investigadoras llegan a la escuela elegida, obtienen la lista de los alumnos inscritos y muestrean sobre ellos. En este escenario hay dos niveles de marcos muestrales (la lista de escuelas de manera inicial y la lista de alumnos por escuela que se obtiene una vez llegas a la escuela elegida). La primera unidad de muestreo (Unidad Primaria de Muestreo) es la escuela; la segunda unidad de muestreo (Unidad Secundaria de Muestreo) son los alumnos.
Unidad de observación El objeto que interesa medir. En el caso de una encuesta dirigida a personas donde se utiliza una lista de casas para encontrar a las personas, la unidad de muestreo es la casa (el objeto de la lista) pero la unidad de observación son las personas que viven dentro de la casa (lo que quiero medir). Una cosa muy parecida (pero no idéntica) es tener una lista de casas y desear estudiar propiedades de la casa (digamos, tamaño). En ese caso la unidad de muestreo y observación coinciden: son la casa.