
Introduction
Introduction.RmdIntroduction
The deltapif package calculates Potential Impact
Fractions (PIF) and Population Attributable Fractions (PAF) for
summary data, along with their confidence intervals, using the delta
method. This vignette provides a practical introduction to the package’s
core functionality.
Core Concepts: PAF and PIF
The Population Attributable Fraction (PAF) answers the question: “What fraction of disease cases in a population would be prevented if we completely eliminated a risk factor?” It represents the maximum possible reduction achievable and is often interpreted as the burden of disease attributed to the exposure.
The Potential Impact Fraction (PIF) is a more general measure. It answers: “What fraction of disease cases would be prevented if we changed exposure from its current distribution to a specific counterfactual scenario?”
PAF is a specific type of PIF where the counterfactual scenario is the theoretical minimum risk exposure level (TMREL). We remark that the TMREL is not always zero. For example, the TMREL for sodium intake is a specific healthy range (e.g., ~1.6g/day), as both too much and too little sodium are harmful. For other exposures, such as smoking, the TMREL can indeed be zero exposure.
Example:
Trieu et al. (2021) estimates the reduction in cardiovascular disease cases if the sodium content in packaged foods was reduced to meet Australian’s government targets. This is a PIF.
Estimating the reduction if sodium consumption was changed to the ideal TMREL of 1.6g/day would be a PAF, representing the maximum achievable benefit.
Why the Delta Method?
This package uses the delta method to calculate confidence intervals for PAF and PIF. This approach offers key advantages:
Distribution-Free: It doesn’t require assumptions about the underlying distribution of the exposure data in the population, which can be difficult to verify and lead to bias if misspecified.
Computational Efficiency:It provides a direct algebraic formula for the variance, making it faster and more stable than simulation-based methods like Monte Carlo.
Transparency: The formula can be derived and understood, offering clarity over “black box” methods.
Key assumption: Independent (summary) data sources.
The deltapif package is designed for a specific, common
scenario in public health:
The estimate of the relative risk (
beta) comes from one source (e.g., a published meta-analysis).The estimate of the exposure prevalence (
p) comes from a separate, independent source (e.g., a national survey).
The delta method implementation here relies on this independence. If
you have individual-level data for exposure the pifpaf package
is more appropriate as it leverages the individual-level variability. If
individual-level exposure and outcome data is available from the same
source the graphPAF
package is ideal.
Examples
Example 1: Estimating the PAF for the proportion of dementia attributable to smoking
The article by M. Lee et al. (2022) estimates the PAF of
dementia associated with 12 risk factors (logrr) in US
adults. The package includes this data as well as the proportion of
exposed individuals in the respective race column (Hispanic, Asian,
Black and White):
data(dementiarisk)#> risk_factor logrr sdlog total hispanic asian black white
#> 1 Less education 0.4637340 0.119140710 10.7 27.1 6.4 10.6 5.5
#> 2 Hearing loss 0.6626880 0.174038430 10.8 13.1 6.9 6.5 10.6
#> 3 TBI 0.6097656 0.090990178 17.1 10.3 6.0 9.2 20.1
#> 4 Hypertension 0.4762342 0.167874478 42.2 38.5 38.5 61.0 39.8
#> 5 Excessive alcohol 0.1655144 0.054020949 3.6 2.0 0.7 2.7 4.2
#> 6 Obesity 0.4700036 0.091750556 44.0 48.3 14.6 54.3 43.5
#> 7 Smoking 0.4637340 0.165486566 8.5 6.9 4.9 11.7 8.4
#> 8 Depression 0.6418539 0.103984905 7.4 10.7 4.3 6.6 7.2
#> 9 Social isolation 0.4510756 0.086112272 11.9 24.0 8.0 12.1 10.8
#> 10 Physical inactivity 0.3293037 0.092961816 62.8 68.6 56.6 73.2 61.3
#> 11 Diabetes 0.4317824 0.075776055 28.6 41.0 44.1 37.2 25.4
#> 12 Air pollution 0.0861777 0.009362766 22.8 44.4 55.2 41.3 17.2In this example, we show how to calculate the population attributable fraction for Smoking among the 4 race groups and then how to calculate the Total Population Attributable Fraction of the overall population.
Notice that Smoking has a log relative risk of:
beta = 0.4637340
with variance of
-
var_beta = 0.0273858(= 0.165486566^2).
Among hispanic individuals 6.9% (p = 0.069) smoke. Hence
their PAF is:
paf_hispanic <- paf(p = 0.069, beta = 0.4637340, var_beta = 0.0273858, var_p = 0,
rr_link = exp, label = "Hispanic")
paf_hispanic
#>
#> ── Population Attributable Fraction: [Hispanic] ──
#>
#> PAF = 3.912% [95% CI: 0.569% to 7.142%]
#> standard_deviation(paf %) = 1.676The other fractions can be computed in the same way noting that 4.9% of non-hispanic asians, 11.7% of non-hispanic blacks and 8.4% of non-hispanic whites smoke:
paf_asian <- paf(p = 0.049, beta = 0.4637340, var_beta = 0.0273858,
var_p = 0, rr_link = exp, label = "Asian")
paf_black <- paf(p = 0.117, beta = 0.4637340, var_beta = 0.0273858,
var_p = 0, rr_link = exp, label = "Black")
paf_white <- paf(p = 0.084, beta = 0.4637340, var_beta = 0.0273858,
var_p = 0, rr_link = exp, label = "White")Combining subpopulations into a total
We can calculate the total population attributable fraction by combining the fractions of the subpopulations weighted by the proportion of the population. According to Wikipedia the distribution in 2020 of the US population by race was as follows:
weights <- c("white" = 0.5784, "hispanic" = 0.1873,
"black" = 0.1205, "asian" = 0.0592)
#Normalized weights to sum to 1
weights <- weights / sum(weights)The paf_total function computes the aggregated
paf of the whole population:
paf_population <- paf_total(paf_white, paf_hispanic, paf_black,
paf_asian, weights = weights, var_weights = 0,
label = "All")
paf_population
#>
#> ── Population Attributable Fraction: [All] ──
#>
#> PAF = 4.663% [95% CI: 4.486% to 4.839%]
#> standard_deviation(paf %) = 1.979
#> ────────────────────────────────── Components: ─────────────────────────────────
#> • 4.722% (sd %: 2.006) --- [White]
#> • 3.912% (sd %: 1.676) --- [Hispanic]
#> • 6.457% (sd %: 2.694) --- [Black]
#> • 2.810% (sd %: 1.218) --- [Asian]
#> ────────────────────────────────────────────────────────────────────────────────where we set var_weights = 0 as no covariance matrix was
known for the race distribution data (it does exist its just not on
Wikipedia).
The paf total implements the following formula:
\[ \textrm{PAF}_{\text{Total}} = w_1 \cdot \text{PAF}_{\text{White}} + w_2 \cdot \text{PAF}_{\text{Hispanic}} + w_3 \cdot \text{PAF}_{\text{Black}} + w_4 \cdot \text{PAF}_{\text{Asian}} \]
where the weights stand for the proportion of the population in each subgroup.
The coef, confint, summary,
and as.data.frame functions have been extended to allow the
user to extract information from a paf (or
pif):
as.data.frame(paf_population)
#> value standard_deviation ci_low ci_up confidence type label
#> 1 0.04662895 0.01979259 0.04486196 0.04839268 0.95 PAF AllAttributable cases can be calculated for example using the estimates
from Dhana et al. (2023). They estimate the
number of people with Alzheimer’s Disease in New York, USA 426.5 (400.2,
452.7) thousand. This implies a variance of
((452.7 - 400.2) / 2*qnorm(0.975))^2 = 2647.005.
attributable_cases(426.5, paf_population, variance = 2647)
#>
#> ── Attributable cases: [All] ──
#>
#> Attributable cases = 19.887 [95% CI: 2.572 to 37.203]
#> standard_deviation(attributable cases) = 883.469Why are we using the log relative risk?
A common question is why in this case we are using the log relative
risk (logrr) with exp link and not the
relative risks directly. The reason depends on what standard deviation
can be properly recovered. Recall that the classic (Wald-type)
confidence intervals should have the same distance from the point
estimate (in this case the RR) to the bounds. We can see
that this does not happen here as for example in the case of
smoking the RR is 1.59 [1.15-2.20] and:
2.20 - 1.59
#> [1] 0.61while
1.59 - 1.15
#> [1] 0.44The distances are not the same!
However in the log-scale they are much more similar:
which suggests that the uncertainty was estimated in the log-scale
and hence we need to use the log relative risk as beta and exponentiate
it (link = exp). Furthermore we can go to the original
paper, check the methodology and conclude that the confidence interval
(and hence the variance!) was estimated using the log-relative risk and
then exponentiated. Hence the uncertainty should be propagated for the
log risk and then exponentiated.
Mathematically the explanation of why this happens is because usually relative risks, odds ratios and hazard ratios are transformed to the log-scale to estimate the confidence intervals. You can see in Wikipedia, for example, the classic formulas for the relative risks CIs and for the odds ratios all involve a log-transform.
Example 2: Estimating the PIF for the proportion of dementia reduced by a 15% reduction in smoking.
M. Lee et al. (2022) also estimates the
proportion of dementia cases that would be reduced by a 15% decrease in
smoking prevalence. This 15% reduction corresponds to multiplying the
current smoking prevalence by 1 - 0.15 = 0.85 specified
with the prevalence under the counterfactual (p_cft)
variable:
pif_hispanic <- pif(p = 0.069, p_cft = 0.069*0.85, beta = 0.4637340, var_beta = 0.0273858,
var_p = 0, rr_link = exp, label = "Hispanic")
pif_asian <- pif(p = 0.049, p_cft = 0.049*0.85, beta = 0.4637340, var_beta = 0.0273858,
var_p = 0, rr_link = exp, label = "Asian")
pif_black <- pif(p = 0.117, p_cft = 0.117*0.85, beta = 0.4637340, var_beta = 0.0273858,
var_p = 0, rr_link = exp, label = "Black")
pif_white <- pif(p = 0.084, p_cft = 0.084*0.85, beta = 0.4637340, var_beta = 0.0273858,
var_p = 0, rr_link = exp, label = "White")The total fraction of the overall population can be aggregated with
pif_total:
pif_population <- pif_total(pif_white, pif_hispanic, pif_black,
pif_asian, weights = weights, var_weights = 0,
label = "All")
pif_population
#>
#> ── Potential Impact Fraction: [All] ──
#>
#> PIF = 0.699% [95% CI: 0.695% to 0.703%]
#> standard_deviation(pif %) = 0.297
#> ────────────────────────────────── Components: ─────────────────────────────────
#> • 0.708% (sd %: 0.301) --- [White]
#> • 0.587% (sd %: 0.251) --- [Hispanic]
#> • 0.969% (sd %: 0.404) --- [Black]
#> • 0.421% (sd %: 0.183) --- [Asian]
#> ────────────────────────────────────────────────────────────────────────────────We can use the as.data.frame function to create a
data.frame with all of the results:
df <- as.data.frame(pif_population, pif_white, pif_black, pif_hispanic, pif_asian)
df
#> value standard_deviation ci_low ci_up confidence type
#> 1 0.006994343 0.002968888 0.0069537857 0.007034899 0.95 PIF
#> 2 0.007082968 0.003009649 0.0011666075 0.012964284 0.95 PIF
#> 3 0.009685883 0.004040705 0.0017344947 0.017573937 0.95 PIF
#> 4 0.005867629 0.002514437 0.0009271875 0.010783639 0.95 PIF
#> 5 0.004214654 0.001826806 0.0006277357 0.007788699 0.95 PIF
#> label
#> 1 All
#> 2 White
#> 3 Black
#> 4 Hispanic
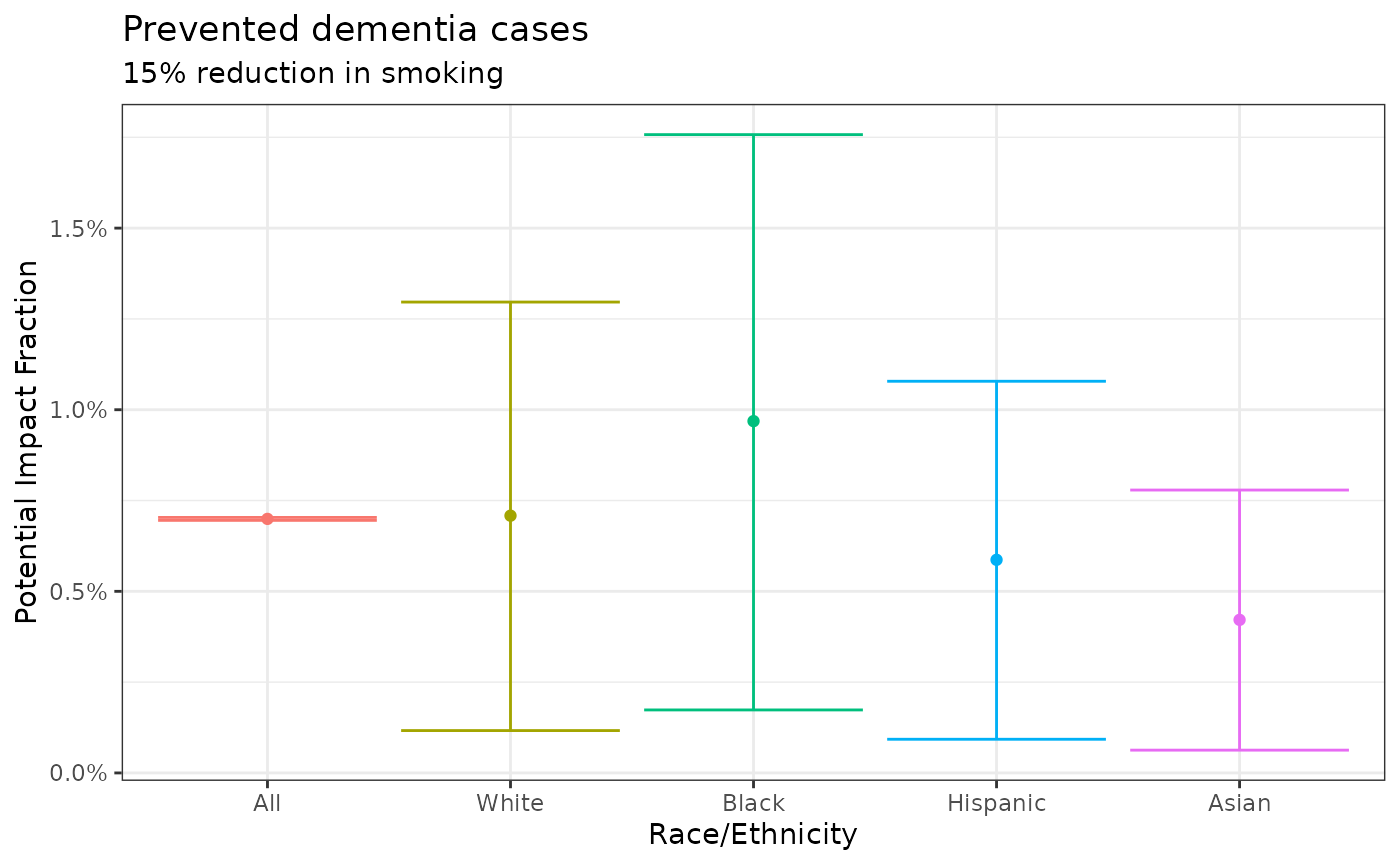
#> 5 AsianGraphically we can visualize the fractions:
if (requireNamespace("ggplot2", quietly = TRUE)){
library(ggplot2)
df$label <- factor(df$label, levels = df$label)
ggplot(df) +
geom_errorbar(aes(x = label, ymin = ci_low, ymax = ci_up, color = label)) +
geom_point(aes(x = label, y = value, color = label)) +
theme_bw() +
labs(
x = "Race/Ethnicity",
y = "Potential Impact Fraction",
title = "Prevented dementia cases",
subtitle = "15% reduction in smoking"
) +
theme(legend.position = "none") +
scale_y_continuous(label = scales::percent_format())
}
Averted cases can be calculated with the same number as before with
the averted_cases function:
averted_cases(426.5, pif_population, variance = 2647)
#>
#> ── Averted cases: [All] ──
#>
#> Averted cases = 2.983 [95% CI: 0.386 to 5.580]
#> standard_deviation(averted cases) = 132.520Example 3: A categorical population attributable fraction
Pandeya et al. (2015) estimate the population attributable fraction of different cancers given distinct levels of alcohol consumption for the Australian population.
The alcohol dataframe included in the package contains
an estimate of the intake of alcohol by sex as well as the proportion of
individuals in each of the intake-categories:
data(alcohol)#> sex alcohol_g median_intake age_18_plus
#> 1 MALE None 0.0 47.2
#> 2 MALE >0-<1 g 0.8 1.4
#> 3 MALE 1-<2g 1.6 2.2
#> 4 MALE 2-<5g 3.2 8.1
#> 5 MALE 5-<10g 7.1 8.1
#> 6 MALE 10-<15g 12.6 6.9
#> 7 MALE 15-<20g 17.4 4.6
#> 8 MALE 20-<30g 24.5 7.3
#> 9 MALE 30-<40g 34.7 4.2
#> 10 MALE 40-<50g 44.2 3.2
#> 11 MALE 50-<60g 54.4 2.0
#> 12 MALE ≥60g 85.2 4.8The relative risk of alcohol varies by consumption level
(alcohol_g). For example in the case of rectal cancer the
estimated relative risk is 1.10 (1.07–1.12) per 10g/day. We will need to
compute the relative risk for each of the consumption level groups using
their median intake as follows:
#Get alcohol intake for men divided by 10 cause RR is per 10g/day
alcohol_men_intake <- c(0, 0.8, 1.6, 3.2, 7.1, 12.6, 17.4, 24.5, 34.7, 44.2, 54.4, 85.2) / 10
#Divided by 10 cause risk is per 10 g/day
relative_risk <- exp(log(1.10)*alcohol_men_intake)
#Divide by 100 to get the prevalence in decimals
prevalence <- c(0.472, 0.014, 0.022, 0.081, 0.081, 0.069, 0.046, 0.073, 0.042, 0.032, 0.02, 0.048)
#Calculate the paf
paf(prevalence, beta = relative_risk, var_p = 0, var_b = 0)
#>
#> ── Population Attributable Fraction: [deltapif-0102908670119104] ──
#>
#> PAF = 70.114% [95% CI: 70.114% to 70.114%]
#> standard_deviation(paf %) = 0.000If we want to add uncertainty we can approximate the covariance of the relative risk as follows:
#Calculate covariance of the betas given by variance*intake_i*intake_j
beta_sd <- (1.12 - 1.07) / (2*qnorm(0.975))
beta_var <- matrix(NA, ncol = length(prevalence), nrow = length(prevalence))
for (k in 1:length(prevalence)){
for (j in 1:length(prevalence)){
beta_var[k,j] <- beta_sd^2*(alcohol_men_intake[j])*(alcohol_men_intake[k])
}
}
#Calculate the paf
paf_males <- paf(prevalence, beta = relative_risk, var_p = 0, var_b = beta_var,
label = "Males")
paf_males
#>
#> ── Population Attributable Fraction: [Males] ──
#>
#> PAF = 70.114% [95% CI: 68.480% to 71.663%]
#> standard_deviation(paf %) = 0.812We can repeat the same process for females:
#Get alcohol intake for women divided by 10 cause RR is per 10g/day
alcohol_female_intake <- c(0, 0.8, 1.6, 3.9, 7.1, 12.6, 17.4, 24.5, 34.7, 44.2, 54.4, 78.1) / 10
#Divided by 10 cause risk is per 10 g/day
relative_risk <- exp(log(1.10)*alcohol_female_intake)
#Divide by 100 to get the prevalence in decimals
prevalence <- c(0.603, 0.02, 0.054, 0.091, 0.081, 0.061, 0.026, 0.034, 0.015, 0.007, 0.003, 0.005)
#Calculate covariance of the betas given by variance*intake_i*intake_j
beta_sd <- (1.12 - 1.07) / (2*qnorm(0.975))
beta_var <- matrix(NA, ncol = length(prevalence), nrow = length(prevalence))
for (k in 1:length(prevalence)){
for (j in 1:length(prevalence)){
beta_var[k,j] <- beta_sd^2*(alcohol_female_intake[j])*(alcohol_female_intake[k])
}
}
#Calculate the paf
paf_females <- paf(prevalence, beta = relative_risk, var_p = 0, var_b = beta_var,
label = "Females")
paf_females
#>
#> ── Population Attributable Fraction: [Females] ──
#>
#> PAF = 65.264% [95% CI: 64.737% to 65.784%]
#> standard_deviation(paf %) = 0.267The total fraction can be computed with paf_total
assuming both males and females are 50% each of the population:
paf_total(paf_males, paf_females, weights = c(0.5, 0.5))
#>
#> ── Population Attributable Fraction: [deltapif-0974069593265456] ──
#>
#> PAF = 67.689% [95% CI: 67.426% to 67.950%]
#> standard_deviation(paf %) = 0.427
#> ────────────────────────────────── Components: ─────────────────────────────────
#> • 70.114% (sd %: 0.812) --- [Males]
#> • 65.264% (sd %: 0.267) --- [Females]
#> ────────────────────────────────────────────────────────────────────────────────Example 4: Combining fractions of different risks into an ensemble
M. Lee et al. (2022) combines multiple population attributable fractions from different risk exposures can be combined into a single fraction. For example, we can create an attributable fraction for behavioral risk factors by joining the fractions for: smoking, physical inactivity, and excesive alcohol consumption into one fraction that represents the reduction in cases if all of these exposures were taken to the level of minimum risk.
For that purpose we calculate each of the fractions separately and
then use the paf_ensemble function to join them. We first
obtain the log-relative risk, its standard deviation, and the total
proportion of individuals exposed (here we highlight the part of the
table):
data(dementiarisk)#> risk_factor logrr sdlog total
#> 5 Excessive alcohol 0.1655144 0.05402095 3.6
#> 7 Smoking 0.4637340 0.16548657 8.5
#> 10 Physical inactivity 0.3293037 0.09296182 62.8We then calculate the population attributable fraction for each:
paf_alcohol <- paf(p = 0.036, beta = 0.1655144, var_beta = 0.05402095^2,
var_p = 0, label = "Alcohol")
paf_smoking <- paf(p = 0.085, beta = 0.4637340, var_beta = 0.16548657^2,
var_p = 0, label = "Smoking")
paf_physical <- paf(p = 0.628, beta = 0.3293037, var_beta = 0.09296182^2,
var_p = 0, label = "Physical Activity")The paf_ensemble function allows to calculate the
ensemble paf by estimating the product:
\[ \textrm{PAF}_{\text{Ensemble}} = 1 - (1 - w_1 \cdot\textrm{PAF}_{\text{Alcohol}})\cdot (1 - w_2 \cdot\textrm{PAF}_{\text{Smoking}})\cdot (1 - w_3\cdot \textrm{PAF}_{\text{Physical}}) \]
where the weights are oftentimes calculated via a communality correction or are set to 1 for disjointed risks. In the case of this paper the communality estimates were:
Physical inactivity: 31.1
Smoking: 5.9
Excessive alcohol: 3.8
hence we can use them as the weights argument:
paf_ensemble(paf_alcohol, paf_physical, paf_smoking,
weights = c(0.038, 0.311, 0.059),
label = "Behavioural factors")
#>
#> ── Population Attributable Fraction: [Behavioural factors] ──
#>
#> PAF = 6.406% [95% CI: 6.202% to 6.610%]
#> standard_deviation(paf %) = 1.627
#> ────────────────────────────────── Components: ─────────────────────────────────
#> • 0.644% (sd %: 0.227) --- [Alcohol]
#> • 19.674% (sd %: 5.236) --- [Physical Activity]
#> • 4.776% (sd %: 2.028) --- [Smoking]
#> ────────────────────────────────────────────────────────────────────────────────Finally, variance among the weights can be implemented with the
var_weights argument providing a variance-covariance
matrix:
#Variance covariance matrix
weight_variance <- matrix(
c( 1.00, 0.21, -0.02,
0.21, 1.00, 0.09,
-0.02, 0.09, 1.00), byrow = TRUE, ncol = 3
)
colnames(weight_variance) <- c("Alcohol", "Physical inactivity", "Smoking")
rownames(weight_variance) <- c("Alcohol", "Physical inactivity", "Smoking")
paf_ensemble(paf_alcohol, paf_physical, paf_smoking,
weights = c(0.038, 0.311, 0.059),
var_weights = weight_variance,
label = "Behavioural factors")
#>
#> ── Population Attributable Fraction: [Behavioural factors] ──
#>
#> PAF = 6.406% [95% CI: 3.807% to 9.005%]
#> standard_deviation(paf %) = 20.699
#> ────────────────────────────────── Components: ─────────────────────────────────
#> • 0.644% (sd %: 0.227) --- [Alcohol]
#> • 19.674% (sd %: 5.236) --- [Physical Activity]
#> • 4.776% (sd %: 2.028) --- [Smoking]
#> ────────────────────────────────────────────────────────────────────────────────Example 6: Ensuring non-negative fractions
S. Lee et al. (2024) show an example
with a relative risk of rr = 7.0 (log relative risk
1.94591) and a log-variance of 0.35. that
results in a negative confidence interval when applying directly the
delta method:
paf(p = 0.05, beta = 1.94, var_beta = 0.591^2, var_p = 0)
#>
#> ── Population Attributable Fraction: [deltapif-048005348427113] ──
#>
#> PAF = 22.955% [95% CI: -5.100% to 43.520%]
#> standard_deviation(paf %) = 12.206The pif and paf functions contain the
logit link option for guaranteeing positivity in the
fraction’s intervals:
paf(p = 0.05, beta = 1.94, var_beta = 0.591^2, var_p = 0, link = "logit")
#>
#> ── Population Attributable Fraction: [deltapif-0604829354215209] ──
#>
#> PAF = 22.955% [95% CI: 7.152% to 53.541%]
#> standard_deviation(paf %) = 12.206We remark that this option is not turned on by default as the positivity of the fraction depends on:
The relative risk being strictly greater than 1.
Epidemiological rationale on why the fraction should be positive.