library(tidyverse)
library(tidymodels)
library(ggfortify) #autoplot para diagnósticos
library(rstanarm) #para bayesiana
library(poissonreg) #modelo Poisson
#Siempre que uses tidymodels
tidymodels_prefer()Regresiones (parte 2)
Si no lo has leído aún ve la parte 1 de regresiones
Paquetes y datos a utilizar
A lo largo de esta sección usaremos los siguientes paquetes:
En general usaremos la filosofía tidymodels para combinar los resultados con el tidyverse. Si quieres saber más de tidymodels te recomiendo checar su libro o su página web.
Modelos lineales generalizados
Regresión Poisson (conteo)
Anteriormente planteamos el modelo
\[ y \sim \textrm{Normal}(\beta_0 + \beta_1 x, \sigma^2) \]
podemos cambiar la distribución normal por una Poisson si tenemos datos de conteo, por ejemplo:
\[ y \sim \textrm{Poisson}(\beta_0 + \beta_1 x) \]
¡Y ya tenemos una regresión Poisson! Ésta no es la clásica pues es bien difícil de controlar numéricamente. La Poisson clásica tiene una exponencial adentro:
\[ y \sim \textrm{Poisson}\big(\exp(\beta_0 + \beta_1 x)\big) \]
Usaremos esta última para los modelos. Para ello nos apoyaremos del engine de glm (por generalized linear model)
Para los datos usaremos la información de Generalized Linear Models for Cross-Classified Data from the WFS. World Fertility Survey Technical Bulletins . Podemos leerlos como sigue:
niños <- read_table("https://data.princeton.edu/wws509/datasets/ceb.dat",
skip = 1, col_names = F)
colnames(niños) <- c("Fila", "dur", "res", "educ", "mean", "var", "n", "y")
niños <- niños %>% mutate(y = round(y))La base contiene la dur la duración del matrimonio, res la residencia (suva, urbano y rural), el nivel educativo educ, la media y la varianza del número de niños nacidos y n la cantidad de mujeres en cada grupo. La variable y contiene el producto de mean*n para obtener el total de niños nacidos para todas las mujeres en cada grupo.
Podemos especificar fácilmente un modelo Poisson para los conteos:
modelo_poisson <- poisson_reg() %>%
set_engine("glm") %>%
fit(y ~ educ, data = niños)podemos obtener el summary:
modelo_poisson %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = y ~ educ, family = stats::poisson, data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-21.757 -8.364 -2.780 3.087 51.573
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.38780 0.01594 338.06 < 2e-16 ***
educnone 0.16257 0.02168 7.50 6.39e-14 ***
educsec+ -2.13937 0.05178 -41.32 < 2e-16 ***
educupper -0.88738 0.02951 -30.07 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 13735.6 on 69 degrees of freedom
Residual deviance: 9076.8 on 66 degrees of freedom
AIC: 9514.3
Number of Fisher Scoring iterations: 5o crear un tibble:
modelo_poisson %>%
extract_fit_engine() %>%
tidy()# A tibble: 4 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 5.39 0.0159 338. 0
2 educnone 0.163 0.0217 7.50 6.39e- 14
3 educsec+ -2.14 0.0518 -41.3 0
4 educupper -0.887 0.0295 -30.1 1.22e-198o también podemos ajustarlo de manera bayesiana:
poisson_reg() %>%
set_engine("stan") %>%
fit(y ~ educ, data = niños) %>%
extract_fit_engine() %>%
summary()Podemos agregar más factores a nuestra regresión. Para ello vale la pena recordar las fórmulas de R:
| Fórmula | Significado |
|---|---|
1 |
El intercepto |
+x |
Agregar la variable x a la regresión |
-x |
Quitar la variable x de la regresión |
x1:x2 |
Interacción entre x1 y x2 |
x1*x2 |
Cruzamiento es lo mismo que poner x1 + x2 + x1:x2 |
I() |
Se utiliza para realizar operaciones aritméticas adentro. Por ejemplo generar una variable que sea x1+ x2 haciendo I(x1 + x2) |
(x | grupo) |
Modelos mixtos donde la pendiente de x depende del grupo (efectos aleatorios) |
En nuestro modelo podemos incluir otras variables (digamos la residencia) agregándolas con suma:
poisson_reg() %>%
set_engine("glm") %>%
fit(y ~ educ + res, data = niños) %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = y ~ educ + res, family = stats::poisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-24.513 -5.069 0.064 3.826 35.524
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 6.02352 0.01759 342.40 < 2e-16 ***
educnone 0.16257 0.02168 7.50 6.4e-14 ***
educsec+ -2.10440 0.05178 -40.64 < 2e-16 ***
educupper -0.88738 0.02951 -30.07 < 2e-16 ***
resSuva -1.43392 0.02783 -51.52 < 2e-16 ***
resurban -1.04901 0.02405 -43.62 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 13735.6 on 69 degrees of freedom
Residual deviance: 5058.4 on 64 degrees of freedom
AIC: 5499.9
Number of Fisher Scoring iterations: 5La educación, sin embargo, es una variable ordinal donde No educación es menor que Sec+ y es menor que Upper. Para ello podemos convertir la variable a factor y especificar el orden:
niños <- niños %>%
mutate(edf = factor(educ, levels = c("none","lower", "sec+","upper"),
ordered = T))
poisson_reg() %>%
set_engine("glm") %>%
fit(y ~ edf + res, data = niños) %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = y ~ edf + res, family = stats::poisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-24.513 -5.069 0.064 3.826 35.524
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.31622 0.01663 319.71 <2e-16 ***
edf.L -1.17488 0.02256 -52.08 <2e-16 ***
edf.Q 0.68980 0.02964 23.27 <2e-16 ***
edf.C 1.17690 0.03533 33.31 <2e-16 ***
resSuva -1.43392 0.02783 -51.52 <2e-16 ***
resurban -1.04901 0.02405 -43.62 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 13735.6 on 69 degrees of freedom
Residual deviance: 5058.4 on 64 degrees of freedom
AIC: 5499.9
Number of Fisher Scoring iterations: 5Podemos agregar también la interacción entre educación y residencia:
poisson_reg() %>%
set_engine("glm") %>%
fit(y ~ edf + res + edf:res, data = niños) %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = y ~ edf + res + edf:res, family = stats::poisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-27.2031 -3.9356 -0.4294 2.5603 31.3342
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.09851 0.02542 200.582 < 2e-16 ***
edf.L -1.57133 0.03346 -46.968 < 2e-16 ***
edf.Q 1.06376 0.05084 20.925 < 2e-16 ***
edf.C 1.55867 0.06364 24.493 < 2e-16 ***
resSuva -1.08021 0.03977 -27.164 < 2e-16 ***
resurban -0.65206 0.03599 -18.117 < 2e-16 ***
edf.L:resSuva 0.72235 0.06338 11.397 < 2e-16 ***
edf.Q:resSuva -0.71608 0.07953 -9.004 < 2e-16 ***
edf.C:resSuva -0.63730 0.09292 -6.859 6.94e-12 ***
edf.L:resurban 1.04382 0.05480 19.048 < 2e-16 ***
edf.Q:resurban -0.77504 0.07198 -10.767 < 2e-16 ***
edf.C:resurban -0.56048 0.08579 -6.533 6.46e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 13735.6 on 69 degrees of freedom
Residual deviance: 4520.8 on 58 degrees of freedom
AIC: 4974.2
Number of Fisher Scoring iterations: 5que es lo mismo que el operador de cruzamiento *:
poisson_reg() %>%
set_engine("glm") %>%
fit(y ~ edf * res, data = niños) %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = y ~ edf * res, family = stats::poisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-27.2031 -3.9356 -0.4294 2.5603 31.3342
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.09851 0.02542 200.582 < 2e-16 ***
edf.L -1.57133 0.03346 -46.968 < 2e-16 ***
edf.Q 1.06376 0.05084 20.925 < 2e-16 ***
edf.C 1.55867 0.06364 24.493 < 2e-16 ***
resSuva -1.08021 0.03977 -27.164 < 2e-16 ***
resurban -0.65206 0.03599 -18.117 < 2e-16 ***
edf.L:resSuva 0.72235 0.06338 11.397 < 2e-16 ***
edf.Q:resSuva -0.71608 0.07953 -9.004 < 2e-16 ***
edf.C:resSuva -0.63730 0.09292 -6.859 6.94e-12 ***
edf.L:resurban 1.04382 0.05480 19.048 < 2e-16 ***
edf.Q:resurban -0.77504 0.07198 -10.767 < 2e-16 ***
edf.C:resurban -0.56048 0.08579 -6.533 6.46e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 13735.6 on 69 degrees of freedom
Residual deviance: 4520.8 on 58 degrees of freedom
AIC: 4974.2
Number of Fisher Scoring iterations: 5En los modelos de Poisson es usual usar un offset dado por el tamaño de la población. Si el offset es \(\lambda\) el modelo se ve como:
\[ y \sim \textrm{Poisson}\big(\lambda\cdot \exp(\beta_0 + \beta_1 x)\big) \]
Usualmente el offset es log(n) donde n es el tamaño de la población. Esto se escribe como:
niños <- niños %>%
mutate(logn = log(n))
poisson_reg() %>%
set_engine("glm") %>%
fit(y ~ edf * res + offset(logn), data = niños) %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = y ~ edf * res + offset(logn), family = stats::poisson,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-19.026 -3.495 1.054 3.626 12.824
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.12094 0.02542 44.099 < 2e-16 ***
edf.L -0.66309 0.03346 -19.820 < 2e-16 ***
edf.Q 0.42450 0.05084 8.350 < 2e-16 ***
edf.C 0.54161 0.06364 8.511 < 2e-16 ***
resSuva -0.08300 0.03977 -2.087 0.03688 *
resurban 0.09584 0.03599 2.663 0.00775 **
edf.L:resSuva -0.11854 0.06338 -1.870 0.06144 .
edf.Q:resSuva -0.03023 0.07953 -0.380 0.70392
edf.C:resSuva 0.04214 0.09292 0.454 0.65016
edf.L:resurban 0.17105 0.05480 3.121 0.00180 **
edf.Q:resurban -0.05337 0.07198 -0.741 0.45849
edf.C:resurban -0.01822 0.08579 -0.212 0.83184
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 3731.9 on 69 degrees of freedom
Residual deviance: 2625.9 on 58 degrees of freedom
AIC: 3079.4
Number of Fisher Scoring iterations: 5Ejercicios
Utilice los datos en la siguiente página. Determine si hay una asociación entre el consumo de cigarros, pipas y puros y la muerte.
Utilice los datos en la siguiente página. Determine si la edad influye en la supervivencia de los tuomores.
Regresión logística y probit
En las regresiones logística y probit el planteamiento es similar sólo que se utilizan para respuestas binarias (0 ó 1). En este caso los modelos son:
\[ y \sim \textrm{Bernoulli}\big(\textrm{logit}(\beta_0 + \beta_1 x)\big) \]
con
\[ \textrm{logit}(p) = \frac{p}{1-p} \]
y
\[ y \sim \textrm{Bernoulli}\big(\Phi(\beta_0 + \beta_1 x)\big) \] donde \(\Phi\) es la función de distribución acumulada de una normal. En ambos casos la especificación es similar:
anticonceptivos <- read_table("https://data.princeton.edu/wws509/datasets/cuse.raw",
skip = 0, col_names = F) %>% uncount(X5)
── Column specification ────────────────────────────────────────────────────────
cols(
X1 = col_double(),
X2 = col_double(),
X3 = col_double(),
X4 = col_double(),
X5 = col_double()
)colnames(anticonceptivos) <- c("age", "education", "wants_more_children",
"using_contraceptive")
anticonceptivos <- anticonceptivos %>%
mutate(
age = case_when(
age == 1 ~ "<25",
age == 2 ~ "25-29",
age == 3 ~ "30-39",
age == 4 ~ "40-49"
)
) %>%
mutate(education = if_else(education == 0, "None", "Some")) %>%
mutate(wants_more_children = if_else(wants_more_children == 0, "No", "More")) %>%
mutate(usa_anticonceptivo = factor(using_contraceptive,
levels = c(0,1), labels = c("No","Yes"))) Podemos checar si la gente está usando o no anticonceptivos en función del grupo de edad con una regresión logística:
modelo_logit <- logistic_reg() %>%
set_engine("glm") %>%
fit(usa_anticonceptivo ~ age + education, data = anticonceptivos) donde podemos ver sus estadísticas por ejemplo con tidy:
modelo_logit %>%
extract_fit_engine() %>%
tidy(conf.int = T, exponentiate = T)# A tibble: 5 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.173 0.166 -10.6 3.61e-26 0.124 0.238
2 age25-29 1.62 0.173 2.78 5.36e- 3 1.16 2.28
3 age30-39 3.14 0.159 7.17 7.77e-13 2.30 4.31
4 age40-49 4.87 0.205 7.72 1.20e-14 3.26 7.30
5 educationSome 1.35 0.122 2.47 1.37e- 2 1.06 1.72 De hecho la logística es sólo un tipo de lineal por lo cual puede hacerse así:
linear_reg() %>%
set_engine("glm", family = binomial(link = "logit")) %>%
fit(using_contraceptive ~ age + education, data = anticonceptivos) %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = using_contraceptive ~ age + education, family = ~binomial(link = "logit"),
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.2313 -0.9304 -0.6474 1.3131 1.9573
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.7562 0.1660 -10.582 < 2e-16 ***
age25-29 0.4821 0.1731 2.784 0.00536 **
age30-39 1.1428 0.1595 7.165 7.77e-13 ***
age40-49 1.5822 0.2051 7.716 1.20e-14 ***
educationSome 0.2999 0.1216 2.465 0.01368 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2003.7 on 1606 degrees of freedom
Residual deviance: 1918.3 on 1602 degrees of freedom
AIC: 1928.3
Number of Fisher Scoring iterations: 4Podemos ponerla directo en Word:
library(gtsummary)
library(flextable)
linear_reg() %>%
set_engine("glm", family = binomial(link = "logit")) %>%
fit(using_contraceptive ~ age + education, data = anticonceptivos) %>%
extract_fit_engine() %>%
tbl_regression(exponentiate = TRUE) %>%
as_flex_table() %>%
save_as_docx(path = "Tabla.docx")Acá hay más opciones para personalizar tu tabla de Word. Ojo tbl_regression sólo está disponible para los modelos que aparecen en la tabla
O bien una probit sólo cambiando el modelo:
linear_reg() %>%
set_engine("glm", family = binomial(link = "probit")) %>%
fit(using_contraceptive ~ age + education, data = anticonceptivos) %>%
extract_fit_engine() %>%
summary()
Call:
stats::glm(formula = using_contraceptive ~ age + education, family = ~binomial(link = "probit"),
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.2279 -0.9322 -0.6484 1.3145 1.9668
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.06014 0.09566 -11.082 < 2e-16 ***
age25-29 0.28020 0.09980 2.808 0.00499 **
age30-39 0.68135 0.09271 7.349 1.99e-13 ***
age40-49 0.95330 0.12262 7.774 7.58e-15 ***
educationSome 0.18071 0.07339 2.462 0.01380 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2003.7 on 1606 degrees of freedom
Residual deviance: 1918.4 on 1602 degrees of freedom
AIC: 1928.4
Number of Fisher Scoring iterations: 4Ejercicio
Descargue la base de datos disponible en este link. La codificación de
imces0si normal o bajo y1si sobrepeso u obesidad. La variableyearsSmokeson los años que lleva la persona fumando cigarrillos ylungCanceres1si ha tenido un diagnóstico de cáncer de pulmón y0si no. Determine si los años que lleva fumando la persona influyen en el diagnóstico. ¿Qué dice la \(R^2\) del ajuste?Repite el análisis de la base de anticonceptivos pero ahora con un modelo bayesiano (
stan). ¿Qué dice elloo?
Regresión Multinomial
Mientras que una logística sirve para clasificar en dos categorías, una multinomial clasifica en múltiples. Leamos los datos:
library(forcats) #para el as_factor
library(haven)
ml <- read_dta("https://stats.idre.ucla.edu/stat/data/hsbdemo.dta")
#Ponerle las etiquetas de stata
ml <- ml %>%
mutate(across(c(female:prog, honors), ~ as_factor(.)))en particular nos interesa estudiar el programa a partir de los valores de ses (nivel socioeconómico) y write (score de su ensayo)
ml %>%
group_by(ses, prog) %>%
tally() %>%
pivot_wider(id_cols = ses, names_from = prog, values_from = n)# A tibble: 3 × 4
# Groups: ses [3]
ses general academic vocation
<fct> <int> <int> <int>
1 low 16 19 12
2 middle 20 44 31
3 high 9 42 7Único cambio es ahora usar multinom_reg para la regresión y el engine default recomendado es nnet (ver más acá)
modelo_multi <- multinom_reg() %>%
set_engine("nnet") %>%
fit(prog ~ ses + write, data = ml)Y listo:
modelo_multi %>%
extract_fit_engine() %>%
tidy(exponentiate = TRUE) # A tibble: 8 × 6
y.level term estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 academic (Intercept) 0.0577 1.17 -2.45 0.0145
2 academic sesmiddle 1.70 0.444 1.20 0.229
3 academic seshigh 3.20 0.514 2.26 0.0237
4 academic write 1.06 0.0214 2.71 0.00682
5 vocation (Intercept) 10.7 1.17 2.01 0.0439
6 vocation sesmiddle 2.28 0.490 1.68 0.0925
7 vocation seshigh 1.20 0.648 0.278 0.781
8 vocation write 0.946 0.0233 -2.39 0.0170 Ejercicio
- Obtén la siguiente base de datos de pingüinos:
library(palmerpenguins)
data(penguins)
pinguinos <- penguinsConstruye un modelo para clasificar un pingüino según su especie (species). Utiliza el modelo para determinar la especie de los siguientes tres pingüinos:
pinguinos_a_determinar <- tibble(
island = c("Torgersen","Torgersen","Dream"),
bill_length_mm = c(20, 18, 14),
flipper_length_mm = c(180, 200, 190)
)Resumen y validación de predicciones
Sección incompleta
En muchos casos al hacer modelos predictivos lo que interesa es solamente si puedes predecir bien el caso. En ese sentido las métricas anteriores no son las mejores.
#Nos interesa predecir diabetes
diabetes <- read_csv(file = "https://raw.githubusercontent.com/MicrosoftDocs/ml-basics/master/data/diabetes.csv")Rows: 15000 Columns: 10
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (10): PatientID, Pregnancies, PlasmaGlucose, DiastolicBloodPressure, Tri...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.#Limpiamos como factor diabetic
diabetes <- diabetes %>%
mutate(Diabetic = factor(Diabetic, levels = c("1","0"),
labels = c("Diabetico","No diabético"))) %>%
select(-PatientID)Visualización:
# Pivot data to a long format
diabetes_select_long <- diabetes %>%
pivot_longer(!Diabetic, names_to = "features", values_to = "values")
ggplot(diabetes_select_long,
aes(x = Diabetic, y = values, fill = features)) +
geom_boxplot() +
facet_wrap(~ features, scales = "free", ncol = 4) +
scale_color_viridis_d(option = "plasma", end = .7) +
theme(legend.position = "none") +
theme_light()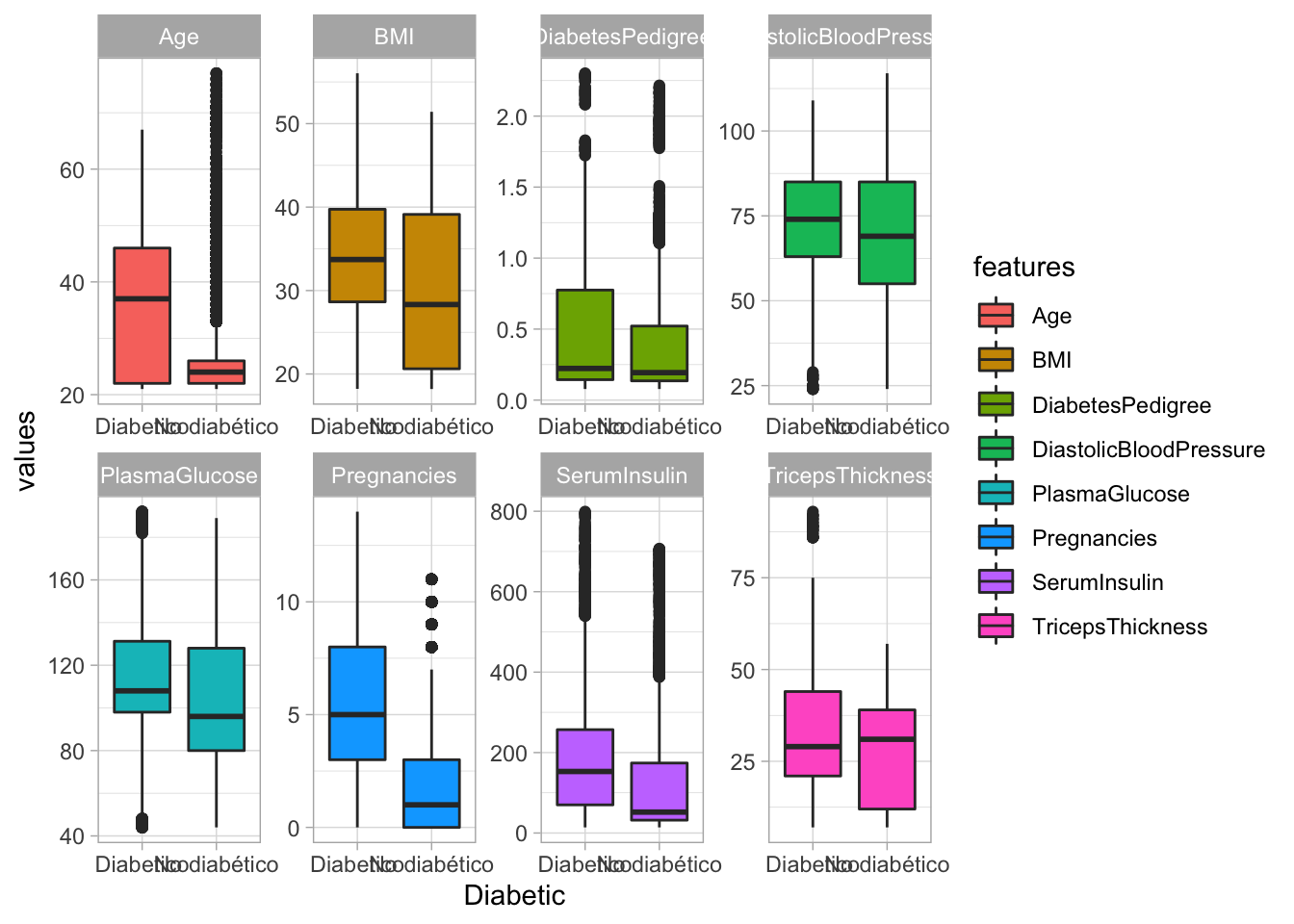
Comenzamos dividiendo los datos
#Seleccionamos 70% para entrenar (usualmente 70-80)
set.seed(2056)
diabetes_split <- diabetes %>%
initial_split(prop = 0.70)
diabetes_train <- training(diabetes_split)
diabetes_test <- testing(diabetes_split)Construimos el modelo:
modelo_logreg <- logistic_reg() %>%
set_engine("glm") Ajustamos:
logreg_fit <- modelo_logreg %>%
fit(Diabetic ~ ., data = diabetes_train) #. significa vs todosChecamos contra los observados:
predichos <- logreg_fit %>%
predict(new_data = diabetes_test)
results <- diabetes_test %>%
select(Diabetic) %>%
bind_cols(predichos)Midamos precisión (positive predictive value), accuracy, sensibilidad (recall), especificidad:
# Combine metrics and evaluate them all at once
eval_metrics <- metric_set(precision, sensitivity,
accuracy, specificity)
eval_metrics(data = results, truth = Diabetic, estimate = .pred_class)# A tibble: 4 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 precision binary 0.754
2 sensitivity binary 0.577
3 accuracy binary 0.789
4 specificity binary 0.901También podemos sacar la matriz de confusión:
conf_mat(data = results, truth = Diabetic, estimate = .pred_class) Truth
Prediction Diabetico No diabético
Diabetico 897 293
No diabético 657 2653También podemos armar nuestra curva roc:
predice_proba <- logreg_fit %>%
predict(new_data = diabetes_test, type = "prob")
results <- results %>%
bind_cols(predice_proba)results %>%
roc_curve(truth = Diabetic, .pred_Diabetico) %>%
autoplot()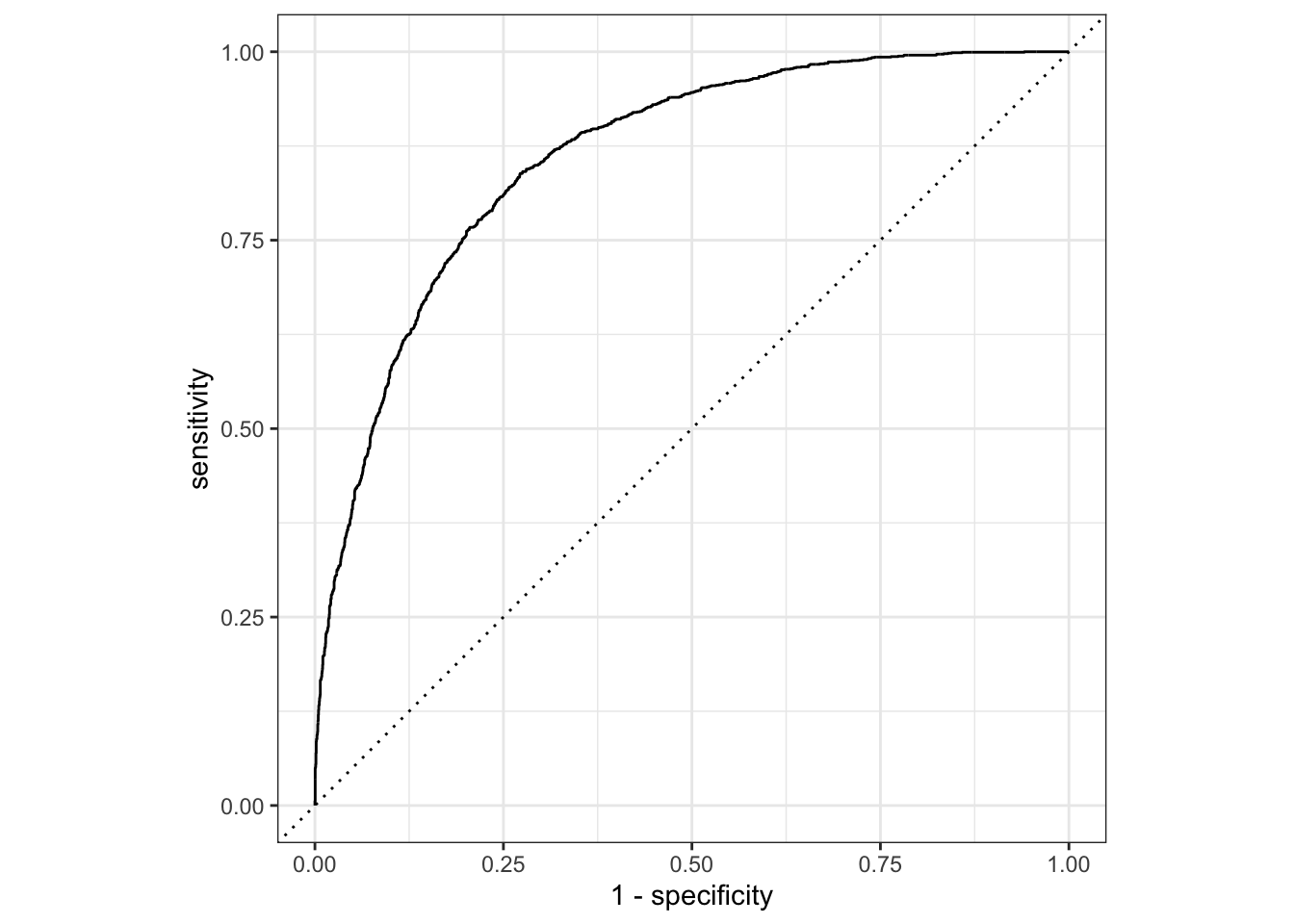
Ejercicio
- Construye tres modelos distintos para predecir diabetes a partir de los siguientes datos sin usar la variable
glucose:
library(mlbench)
data(PimaIndiansDiabetes)
diabedatos <- PimaIndiansDiabetesTus modelos pueden ser logísticos pero al menos uno de los tres que sea un árbol en mode = "classification" (opciones: bart, random_forest, boost_tree, decision_tree, bag_tree)
Utiliza métricas (como sensibilidad, especificidad, etc) sobre el para decidir cuál es el mejor modelo.
Series de tiempo
Sección incompleta
Análisis preliminar
library(modeltime)
library(timetk)
library(lubridate)Casos de campylobacter en Alemania (copia y pega)
library(readxl)
url <- "https://github.com/epirhandbook/Epi_R_handbook/raw/master/data/time_series/campylobacter_germany.xlsx"
destfile <- "campylobacter_germany.xlsx"
curl::curl_download(url, destfile)
campylobacter_germany <- read_excel(destfile)Veamos la info:
ggplot(campylobacter_germany) +
geom_line(aes(x = date, y = case)) +
theme_light()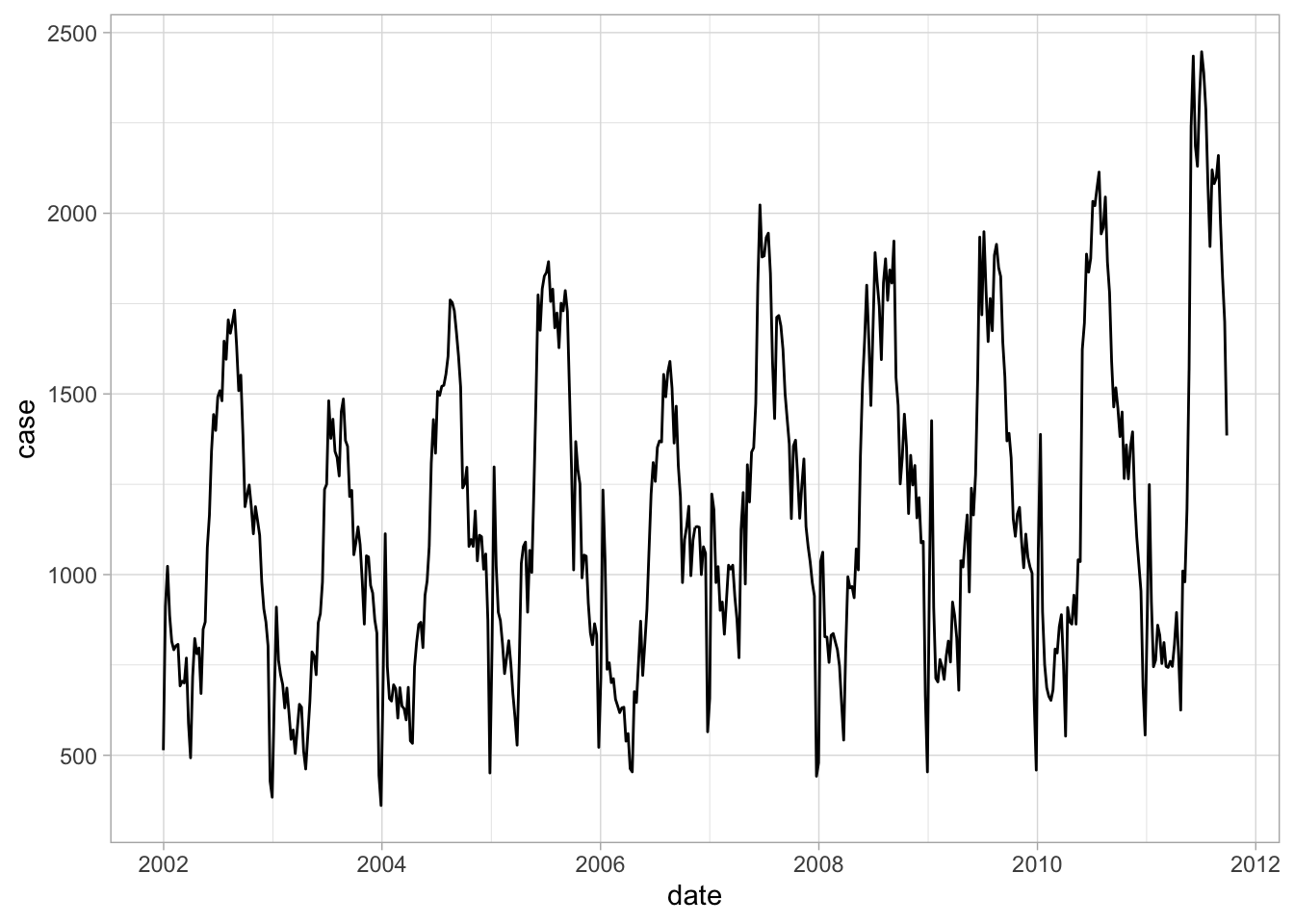
Otra forma:
campylobacter_germany %>%
plot_time_series(date, case, .interactive = T)Partes de una serie de tiempo clásica:
campylobacter_germany %>%
plot_acf_diagnostics(date, case, .interactive = T, .lags = 52)Warning: `gather_()` was deprecated in tidyr 1.2.0.
Please use `gather()` instead.campylobacter_germany %>%
plot_seasonal_diagnostics(date, case, .interactive = T)campylobacter_germany %>%
plot_stl_diagnostics(date, case, .interactive = F)frequency = 13 observations per 1 quartertrend = 53 observations per 1 year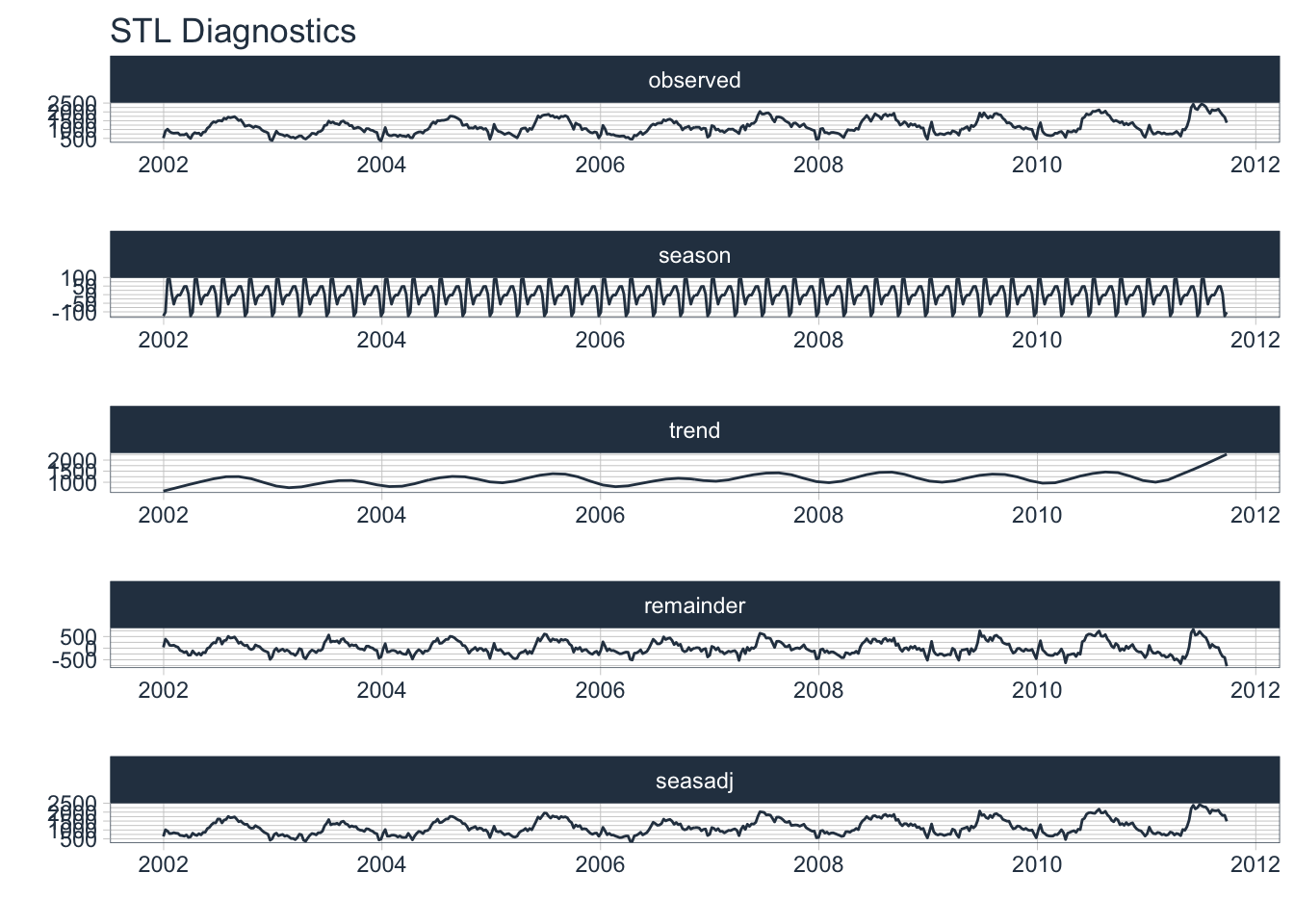
#Como no se ve completo
ggsave("Diags.pdf", width = 10, height = 25)Modelos
En esta sección haremos arima_reg() y linear_reg(). En teoría el arima debería ser mejor que una regresión lineal.
#Para decidir el modelo primero obtenemos splits
splits <- initial_time_split(campylobacter_germany, prop = 0.8)
entrena <- training(splits)
testea <- testing(splits)
#Ajuste de un ARIMA
modelo_ARIMA <- arima_reg() %>%
set_engine(engine = "auto_arima") %>%
fit(case ~ date + factor(month(date, label = TRUE),
ordered = FALSE), data = entrena)frequency = 13 observations per 1 quarter#Regresión lineal con mes como cofactor
model_lm <- linear_reg() %>%
set_engine("lm") %>%
fit(case ~ as.numeric(date) +
factor(month(date, label = TRUE), ordered = FALSE),
data = entrena)
#Junto mis modelos
models_tbl <- modeltime_table(
modelo_ARIMA, model_lm
)
#Veo contra el test
calibration_tbl <- models_tbl %>%
modeltime_calibrate(new_data = testea)
#Veo
calibration_tbl %>%
modeltime_forecast(
new_data = testea,
actual_data = campylobacter_germany
) %>%
plot_modeltime_forecast(
.interactive = T
)#Tabulo métricas
calibration_tbl %>%
modeltime_accuracy() %>%
table_modeltime_accuracy(
.interactive = T
)#Reajuste y predicción del futuro
refit_tbl <- calibration_tbl %>%
modeltime_refit(data = campylobacter_germany)frequency = 13 observations per 1 quarterfuturo <- refit_tbl %>%
modeltime_forecast(h = "3 years",
actual_data = campylobacter_germany)
futuro %>%
filter(.model_desc != "UPDATE: REGRESSION WITH ARIMA(3,1,0)(0,0,1)[13] ERRORS") %>%
plot_modeltime_forecast(
.interactive = T
)Ejercicio
La siguiente base de datos contiene los registros de dengue en México de 2017 a la fecha. Las variables son fecha (proxy de semana epidemológica) y nraw (casos de dengue en la semana). n es un suavizamiento con media móvil, logn y log_nraw representan los logaritmos de la media móvil n y de nraw respectivamente. Las variables t y n.value se deben ignorar.
Ajuste al menos dos modelos distintos uno de ellos
prophet_regpara determinar cuántos casos de dengue habrán hasta que termine el año.
dengue <- read_csv("https://media.githubusercontent.com/media/RodrigoZepeda/DengueMX/lognormal/datos-limpios/dengue_for_model_mx.csv") %>%
filter(fecha >= as.Date("2017/01/01"))Rows: 395 Columns: 7
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (6): n, n.value, nraw, t, logn, log_nraw
date (1): fecha
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Sistema
sessioninfo::session_info()─ Session info ───────────────────────────────────────────────────────────────
setting value
version R version 4.2.1 (2022-06-23)
os macOS Big Sur ... 10.16
system x86_64, darwin17.0
ui X11
language (EN)
collate en_US.UTF-8
ctype en_US.UTF-8
tz America/Mexico_City
date 2022-10-05
pandoc 2.19.2 @ /Applications/RStudio.app/Contents/MacOS/quarto/bin/tools/ (via rmarkdown)
─ Packages ───────────────────────────────────────────────────────────────────
package * version date (UTC) lib source
assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.2.0)
backports 1.4.1 2021-12-13 [1] CRAN (R 4.2.0)
base64enc 0.1-3 2015-07-28 [1] CRAN (R 4.2.0)
bayesplot 1.9.0 2022-03-10 [1] CRAN (R 4.2.0)
bit 4.0.4 2020-08-04 [1] CRAN (R 4.2.0)
bit64 4.0.5 2020-08-30 [1] CRAN (R 4.2.0)
boot 1.3-28 2021-05-03 [1] CRAN (R 4.2.1)
broom * 1.0.1 2022-08-29 [1] CRAN (R 4.2.0)
broom.helpers 1.9.0 2022-09-23 [1] CRAN (R 4.2.0)
cachem 1.0.6 2021-08-19 [1] CRAN (R 4.2.0)
callr 3.7.2 2022-08-22 [1] CRAN (R 4.2.0)
cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.2.0)
class 7.3-20 2022-01-16 [1] CRAN (R 4.2.1)
cli 3.4.1 2022-09-23 [1] CRAN (R 4.2.0)
codetools 0.2-18 2020-11-04 [1] CRAN (R 4.2.1)
colorspace 2.0-3 2022-02-21 [1] CRAN (R 4.2.0)
colourpicker 1.1.1 2021-10-04 [1] CRAN (R 4.2.0)
conflicted 1.1.0 2021-11-26 [1] CRAN (R 4.2.0)
crayon 1.5.2 2022-09-29 [1] CRAN (R 4.2.0)
crosstalk 1.2.0 2021-11-04 [1] CRAN (R 4.2.0)
curl 4.3.2 2021-06-23 [1] CRAN (R 4.2.0)
data.table 1.14.2 2021-09-27 [1] CRAN (R 4.2.0)
DBI 1.1.3 2022-06-18 [1] CRAN (R 4.2.0)
dbplyr 2.2.1 2022-06-27 [1] CRAN (R 4.2.0)
dials * 1.0.0 2022-06-14 [1] CRAN (R 4.2.0)
DiceDesign 1.9 2021-02-13 [1] CRAN (R 4.2.0)
digest 0.6.29 2021-12-01 [1] CRAN (R 4.2.0)
dplyr * 1.0.10 2022-09-01 [1] CRAN (R 4.2.0)
DT 0.25 2022-09-12 [1] CRAN (R 4.2.0)
dygraphs 1.1.1.6 2018-07-11 [1] CRAN (R 4.2.0)
ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.2.0)
evaluate 0.16 2022-08-09 [1] CRAN (R 4.2.0)
fansi 1.0.3 2022-03-24 [1] CRAN (R 4.2.0)
farver 2.1.1 2022-07-06 [1] CRAN (R 4.2.0)
fastmap 1.1.0 2021-01-25 [1] CRAN (R 4.2.0)
flextable * 0.8.2 2022-09-26 [1] CRAN (R 4.2.0)
forcats * 0.5.2 2022-08-19 [1] CRAN (R 4.2.0)
foreach 1.5.2 2022-02-02 [1] CRAN (R 4.2.0)
forecast 8.18 2022-10-02 [1] CRAN (R 4.2.0)
fracdiff 1.5-1 2020-01-24 [1] CRAN (R 4.2.0)
fs 1.5.2 2021-12-08 [1] CRAN (R 4.2.0)
furrr 0.3.1 2022-08-15 [1] CRAN (R 4.2.0)
future 1.28.0 2022-09-02 [1] CRAN (R 4.2.0)
future.apply 1.9.1 2022-09-07 [1] CRAN (R 4.2.0)
gargle 1.2.1 2022-09-08 [1] CRAN (R 4.2.0)
gdtools 0.2.4 2022-02-14 [1] CRAN (R 4.2.0)
generics 0.1.3 2022-07-05 [1] CRAN (R 4.2.0)
ggfortify * 0.4.14 2022-01-03 [1] CRAN (R 4.2.0)
ggplot2 * 3.3.6 2022-05-03 [1] CRAN (R 4.2.0)
ggridges 0.5.4 2022-09-26 [1] CRAN (R 4.2.0)
globals 0.16.1 2022-08-28 [1] CRAN (R 4.2.0)
glue 1.6.2 2022-02-24 [1] CRAN (R 4.2.0)
googledrive 2.0.0 2021-07-08 [1] CRAN (R 4.2.0)
googlesheets4 1.0.1 2022-08-13 [1] CRAN (R 4.2.0)
gower 1.0.0 2022-02-03 [1] CRAN (R 4.2.0)
GPfit 1.0-8 2019-02-08 [1] CRAN (R 4.2.0)
gridExtra 2.3 2017-09-09 [1] CRAN (R 4.2.0)
gt 0.7.0 2022-08-25 [1] CRAN (R 4.2.0)
gtable 0.3.1 2022-09-01 [1] CRAN (R 4.2.0)
gtools 3.9.3 2022-07-11 [1] CRAN (R 4.2.0)
gtsummary * 1.6.2 2022-09-30 [1] CRAN (R 4.2.0)
hardhat 1.2.0 2022-06-30 [1] CRAN (R 4.2.0)
haven * 2.5.1 2022-08-22 [1] CRAN (R 4.2.0)
hms 1.1.2 2022-08-19 [1] CRAN (R 4.2.0)
htmltools 0.5.3 2022-07-18 [1] CRAN (R 4.2.0)
htmlwidgets 1.5.4 2021-09-08 [1] CRAN (R 4.2.0)
httpuv 1.6.6 2022-09-08 [1] CRAN (R 4.2.0)
httr 1.4.4 2022-08-17 [1] CRAN (R 4.2.0)
igraph 1.3.5 2022-09-22 [1] CRAN (R 4.2.0)
infer * 1.0.3 2022-08-22 [1] CRAN (R 4.2.0)
inline 0.3.19 2021-05-31 [1] CRAN (R 4.2.0)
ipred 0.9-13 2022-06-02 [1] CRAN (R 4.2.0)
iterators 1.0.14 2022-02-05 [1] CRAN (R 4.2.0)
janitor 2.1.0 2021-01-05 [1] CRAN (R 4.2.0)
jsonlite 1.8.2 2022-10-02 [1] CRAN (R 4.2.0)
knitr 1.40 2022-08-24 [1] CRAN (R 4.2.0)
labeling 0.4.2 2020-10-20 [1] CRAN (R 4.2.0)
labelled 2.10.0 2022-09-14 [1] CRAN (R 4.2.0)
later 1.3.0 2021-08-18 [1] CRAN (R 4.2.0)
lattice 0.20-45 2021-09-22 [1] CRAN (R 4.2.1)
lava 1.6.10 2021-09-02 [1] CRAN (R 4.2.0)
lazyeval 0.2.2 2019-03-15 [1] CRAN (R 4.2.0)
lhs 1.1.5 2022-03-22 [1] CRAN (R 4.2.0)
lifecycle 1.0.2 2022-09-09 [1] CRAN (R 4.2.0)
listenv 0.8.0 2019-12-05 [1] CRAN (R 4.2.0)
lme4 1.1-30 2022-07-08 [1] CRAN (R 4.2.0)
lmtest 0.9-40 2022-03-21 [1] CRAN (R 4.2.0)
loo 2.5.1 2022-03-24 [1] CRAN (R 4.2.0)
lubridate * 1.8.0 2021-10-07 [1] CRAN (R 4.2.0)
magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.2.0)
markdown 1.1 2019-08-07 [1] CRAN (R 4.2.0)
MASS 7.3-58.1 2022-08-03 [1] CRAN (R 4.2.0)
Matrix 1.5-1 2022-09-13 [1] CRAN (R 4.2.0)
matrixStats 0.62.0 2022-04-19 [1] CRAN (R 4.2.0)
memoise 2.0.1 2021-11-26 [1] CRAN (R 4.2.0)
mime 0.12 2021-09-28 [1] CRAN (R 4.2.0)
miniUI 0.1.1.1 2018-05-18 [1] CRAN (R 4.2.0)
minqa 1.2.4 2014-10-09 [1] CRAN (R 4.2.0)
mlbench * 2.1-3 2021-01-29 [1] CRAN (R 4.2.0)
modeldata * 1.0.1 2022-09-06 [1] CRAN (R 4.2.0)
modelr 0.1.9 2022-08-19 [1] CRAN (R 4.2.0)
modeltime * 1.2.2 2022-06-07 [1] CRAN (R 4.2.0)
munsell 0.5.0 2018-06-12 [1] CRAN (R 4.2.0)
nlme 3.1-159 2022-08-09 [1] CRAN (R 4.2.0)
nloptr 2.0.3 2022-05-26 [1] CRAN (R 4.2.0)
nnet 7.3-18 2022-09-28 [1] CRAN (R 4.2.0)
officer 0.4.4 2022-09-09 [1] CRAN (R 4.2.0)
palmerpenguins * 0.1.1 2022-08-15 [1] CRAN (R 4.2.0)
parallelly 1.32.1 2022-07-21 [1] CRAN (R 4.2.0)
parsnip * 1.0.2 2022-10-01 [1] CRAN (R 4.2.0)
pillar 1.8.1 2022-08-19 [1] CRAN (R 4.2.0)
pkgbuild 1.3.1 2021-12-20 [1] CRAN (R 4.2.0)
pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.2.0)
plotly 4.10.0 2021-10-09 [1] CRAN (R 4.2.0)
plyr 1.8.7 2022-03-24 [1] CRAN (R 4.2.0)
poissonreg * 1.0.1 2022-08-22 [1] CRAN (R 4.2.0)
prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.2.0)
processx 3.7.0 2022-07-07 [1] CRAN (R 4.2.0)
prodlim 2019.11.13 2019-11-17 [1] CRAN (R 4.2.0)
promises 1.2.0.1 2021-02-11 [1] CRAN (R 4.2.0)
ps 1.7.1 2022-06-18 [1] CRAN (R 4.2.0)
purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.2.0)
quadprog 1.5-8 2019-11-20 [1] CRAN (R 4.2.0)
quantmod 0.4.20 2022-04-29 [1] CRAN (R 4.2.0)
R6 2.5.1 2021-08-19 [1] CRAN (R 4.2.0)
ragg 1.2.3 2022-09-29 [1] CRAN (R 4.2.0)
Rcpp * 1.0.9 2022-07-08 [1] CRAN (R 4.2.0)
RcppParallel 5.1.5 2022-01-05 [1] CRAN (R 4.2.0)
reactable 0.3.0 2022-05-26 [1] CRAN (R 4.2.0)
reactR 0.4.4 2021-02-22 [1] CRAN (R 4.2.0)
readr * 2.1.3 2022-10-01 [1] CRAN (R 4.2.0)
readxl * 1.4.1 2022-08-17 [1] CRAN (R 4.2.0)
recipes * 1.0.1 2022-07-07 [1] CRAN (R 4.2.0)
reprex 2.0.2 2022-08-17 [1] CRAN (R 4.2.0)
reshape2 1.4.4 2020-04-09 [1] CRAN (R 4.2.0)
rlang 1.0.6 2022-09-24 [1] CRAN (R 4.2.0)
rmarkdown 2.16 2022-08-24 [1] CRAN (R 4.2.0)
rpart 4.1.16 2022-01-24 [1] CRAN (R 4.2.1)
rsample * 1.1.0 2022-08-08 [1] CRAN (R 4.2.0)
rstan 2.21.7 2022-09-08 [1] CRAN (R 4.2.0)
rstanarm * 2.21.3 2022-04-09 [1] CRAN (R 4.2.0)
rstantools 2.2.0 2022-04-08 [1] CRAN (R 4.2.0)
rstudioapi 0.14 2022-08-22 [1] CRAN (R 4.2.0)
rvest 1.0.3 2022-08-19 [1] CRAN (R 4.2.0)
scales * 1.2.1 2022-08-20 [1] CRAN (R 4.2.0)
sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.2.0)
shiny 1.7.2 2022-07-19 [1] CRAN (R 4.2.0)
shinyjs 2.1.0 2021-12-23 [1] CRAN (R 4.2.0)
shinystan 2.6.0 2022-03-03 [1] CRAN (R 4.2.0)
shinythemes 1.2.0 2021-01-25 [1] CRAN (R 4.2.0)
snakecase 0.11.0 2019-05-25 [1] CRAN (R 4.2.0)
StanHeaders 2.21.0-7 2020-12-17 [1] CRAN (R 4.2.0)
stringi 1.7.8 2022-07-11 [1] CRAN (R 4.2.0)
stringr * 1.4.1 2022-08-20 [1] CRAN (R 4.2.0)
survival 3.4-0 2022-08-09 [1] CRAN (R 4.2.0)
systemfonts 1.0.4 2022-02-11 [1] CRAN (R 4.2.0)
textshaping 0.3.6 2021-10-13 [1] CRAN (R 4.2.0)
threejs 0.3.3 2020-01-21 [1] CRAN (R 4.2.0)
tibble * 3.1.8 2022-07-22 [1] CRAN (R 4.2.0)
tidymodels * 1.0.0 2022-07-13 [1] CRAN (R 4.2.0)
tidyr * 1.2.1 2022-09-08 [1] CRAN (R 4.2.0)
tidyselect 1.1.2 2022-02-21 [1] CRAN (R 4.2.0)
tidyverse * 1.3.2 2022-07-18 [1] CRAN (R 4.2.0)
timeDate 4021.106 2022-09-30 [1] CRAN (R 4.2.0)
timetk * 2.8.1 2022-05-31 [1] CRAN (R 4.2.0)
tseries 0.10-51 2022-05-01 [1] CRAN (R 4.2.0)
TTR 0.24.3 2021-12-12 [1] CRAN (R 4.2.0)
tune * 1.0.0 2022-07-07 [1] CRAN (R 4.2.0)
tzdb 0.3.0 2022-03-28 [1] CRAN (R 4.2.0)
urca 1.3-3 2022-08-29 [1] CRAN (R 4.2.0)
utf8 1.2.2 2021-07-24 [1] CRAN (R 4.2.0)
uuid 1.1-0 2022-04-19 [1] CRAN (R 4.2.0)
vctrs 0.4.2 2022-09-29 [1] CRAN (R 4.2.0)
viridisLite 0.4.1 2022-08-22 [1] CRAN (R 4.2.0)
vroom 1.6.0 2022-09-30 [1] CRAN (R 4.2.0)
withr 2.5.0 2022-03-03 [1] CRAN (R 4.2.0)
workflows * 1.1.0 2022-09-26 [1] CRAN (R 4.2.0)
workflowsets * 1.0.0 2022-07-12 [1] CRAN (R 4.2.0)
xfun 0.33 2022-09-12 [1] CRAN (R 4.2.0)
xml2 1.3.3 2021-11-30 [1] CRAN (R 4.2.0)
xtable 1.8-4 2019-04-21 [1] CRAN (R 4.2.0)
xts 0.12.1 2020-09-09 [1] CRAN (R 4.2.0)
yaml 2.3.5 2022-02-21 [1] CRAN (R 4.2.0)
yardstick * 1.1.0 2022-09-07 [1] CRAN (R 4.2.0)
zip 2.2.1 2022-09-08 [1] CRAN (R 4.2.0)
zoo 1.8-11 2022-09-17 [1] CRAN (R 4.2.0)
[1] /Library/Frameworks/R.framework/Versions/4.2/Resources/library
──────────────────────────────────────────────────────────────────────────────