Tutorial: Crear mapas de calor (intensidad) para México

Resumen

En esta entrada discutiremos cómo generar mapas de calor (intensidad) de un proceso puntual en el espacio usando un mapa de México

Mapa de calor

En esta entrada aprenderemos a hacer un mapa de calor como el que sigue:

Mapa de calor de la Ciudad de México muestra mayor intensidad al norte

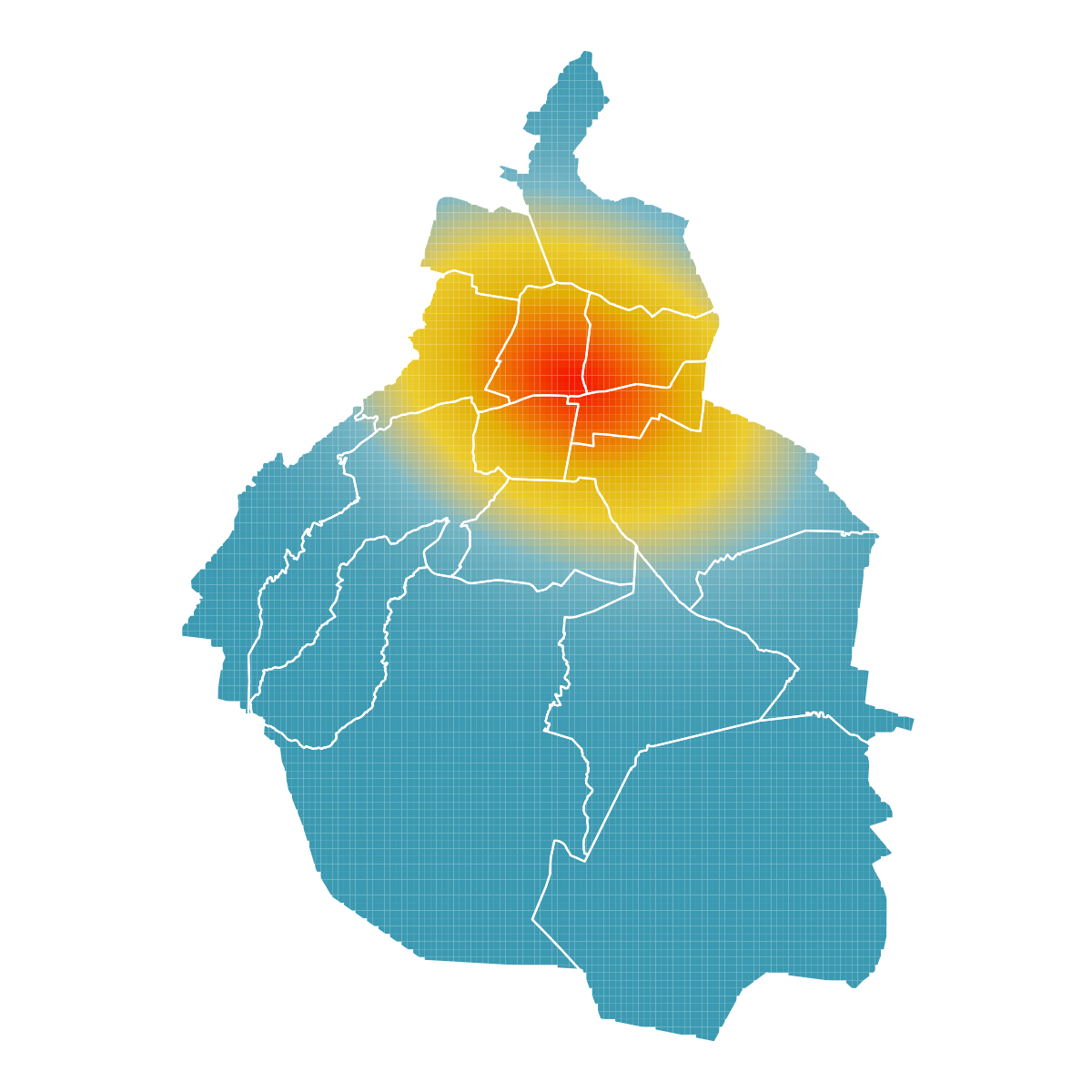
Usaremos los siguientes paquetes para generar el mapa:

# Lectura de los paquetes
pacman::p_load(tidyverse, sf, spatstat, stars, wesanderson)

Carpetas de investigación de la Ciudad de México

Para el propósito de este análisis utilizaremos las carpetas de investigación de la Fiscalía de la Ciudad de México la cual contiene información “de las víctimas de los delitos en las carpetas de investigación de la Fiscalía General de Justicia (FGJ)”.

# Link de datos de la fiscalía de CDMX
url <- paste0("https://datos.cdmx.gob.mx/dataset/7593b324-6010-44f7-",
              "8132-cb8b2276c842/resource/68304227-862f-4b86-8382-e35",
              "b317a7c39/download/da_victimas_19-20.csv")
df_fiscalia <- read_csv(url, show_col_types = F)

La base se ve así:

idCarpeta	Año_inicio	Mes_inicio	FechaInicio	Delito	Categoria	Sexo	Edad	TipoPersona	CalidadJuridica	competencia	Año_hecho	Mes_hecho	FechaHecho	HoraHecho	HoraInicio	alcaldia_hechos	municipio_hechos	colonia_datos	fgj_colonia_registro	latitud	longitud
numeric	numeric	character	Date	character	character	character	numeric	character	character	character	numeric	character	Date	hms	hms	character	character	character	character	numeric	numeric
8,324,429	2,019	Enero	2019-01-04	FRAUDE	DELITO DE BAJO IMPACTO	Masculino	62	FISICA	OFENDIDO	FUERO COMUN	2,018	Agosto	2018-08-29	43,200.0	44,340.0	ALVARO OBREGON		GUADALUPE INN	GUADALUPE INN	19.4	-99.2
8,324,430	2,019	Enero	2019-01-04	PRODUCCIÓN, IMPRESIÓN, ENAJENACIÓN, DISTRIBUCIÓN, ALTERACIÓN O FALSIFICACIÓN DE TÍTULOS AL PORTADOR, DOCUMENTOS DE CRÉDITO PÚBLICOS O VALES DE CANJE	DELITO DE BAJO IMPACTO	Femenino	38	FISICA	VICTIMA Y DENUNCIANTE	FUERO COMUN	2,018	Diciembre	2018-12-15	54,000.0	44,400.0	AZCAPOTZALCO		VICTORIA DE LAS DEMOCRACIAS	VICTORIA DE LAS DEMOCRACIAS	19.5	-99.2
8,324,431	2,019	Enero	2019-01-04	ROBO A TRANSEUNTE SALIENDO DEL BANCO CON VIOLENCIA	ROBO A CUENTAHABIENTE SALIENDO DEL CAJERO CON VIOLENCIA	Masculino	42	FISICA	VICTIMA Y DENUNCIANTE	FUERO COMUN	2,018	Diciembre	2018-12-22	55,800.0	44,580.0	COYOACAN		COPILCO EL BAJO	COPILCO UNIVERSIDAD ISSSTE	19.3	-99.2
8,324,435	2,019	Enero	2019-01-04	ROBO DE VEHICULO DE SERVICIO PARTICULAR SIN VIOLENCIA	ROBO DE VEHÍCULO CON Y SIN VIOLENCIA	Masculino	35	FISICA	VICTIMA Y DENUNCIANTE	FUERO COMUN	2,019	Enero	2019-01-04	21,600.0	44,820.0	IZTACALCO		PANTITLAN V	AGRÍCOLA PANTITLAN	19.4	-99.1
8,324,438	2,019	Enero	2019-01-04	ROBO DE MOTOCICLETA SIN VIOLENCIA	ROBO DE VEHÍCULO CON Y SIN VIOLENCIA	Masculino		FISICA	VICTIMA	FUERO COMUN	2,019	Enero	2019-01-03	72,000.0	45,300.0	IZTAPALAPA		LAS AMERICAS (U HAB)	PROGRESISTA	19.4	-99.1
8,324,442	2,019	Enero	2019-01-04	PRODUCCIÓN, IMPRESIÓN, ENAJENACIÓN, DISTRIBUCIÓN, ALTERACIÓN O FALSIFICACIÓN DE TÍTULOS AL PORTADOR, DOCUMENTOS DE CRÉDITO PÚBLICOS O VALES DE CANJE	DELITO DE BAJO IMPACTO	Femenino	42	FISICA	OFENDIDO	FUERO COMUN	2,018	Octubre	2018-10-12	64,800.0	45,480.0	COYOACAN		LOS REYES (PBLO)	PUEBLO DE LOS REYES	19.3	-99.2
n: 6

Las columnas importantes para este análisis son latitud y longitud las cuales refieren a las coordenadas de los eventos. Por ahora utilizaremos sólo las carpetas sobre ROBO A PASAJERO.

df_robos <- df_fiscalia |> 
  filter(str_detect(Delito, "ROBO A PASAJERO")) |>
  distinct(latitud, longitud)

Lo cual nos deja una lista de coordenadas:

latitud	longitud
numeric	numeric
19.4	-99.1
19.3	-99.0
19.4	-99.2
19.4	-99.1
19.4	-99.1
19.5	-99.1
n: 6

Mapa de la CDMX

El mapa de la Ciudad de México lo obtendremos del Instituto Nacional de Estadística y Geografía. En particular éste puede encontrarse en Temas > Marco Geoestadístico y luego seleccionando el marco más reciente y la entidad elegida (o el Nacional que baja todas las entidades).

Nota

Si quieres replicar éste ejercicio para un mapa específico de otra región no cubierta por el INEGI una fuente con un amplia librería de mapas es la Universidad de Berkeley

Una vez descargado el mapa (o descargándolo con el código a continuación) leemos el archivo con la función read_sf del paquete sf (simple features).

# Descargamos del inegi los datos
mapa_archivo <- tempfile(fileext = ".zip")
mapa_dir     <- tempdir()
url_mapa <- paste0("https://www.inegi.org.mx/contenidos/productos/prod_serv",
                   "/contenidos/espanol/bvinegi/productos/geografia/marcogeo/",
                   "889463770541/09_ciudaddemexico.zip")
download.file(url_mapa, mapa_archivo, method = "curl") #Quizá curl no funcione en windows

# Leemos el mapa
unzip(mapa_archivo, exdir = mapa_dir)

# Leemos los datos
cdmx <- read_sf(file.path(mapa_dir,"09_ciudaddemexico","conjunto_de_datos","09mun.shp"))

El resultado de leer los datos en cdmx es un tibble que contiene los polígonos demarcando los municipios de la CDMX. Podemos ver la gráfica de esto con geom_sf:

ggplot(cdmx) +
  geom_sf(aes(geometry = geometry)) +
  theme_minimal()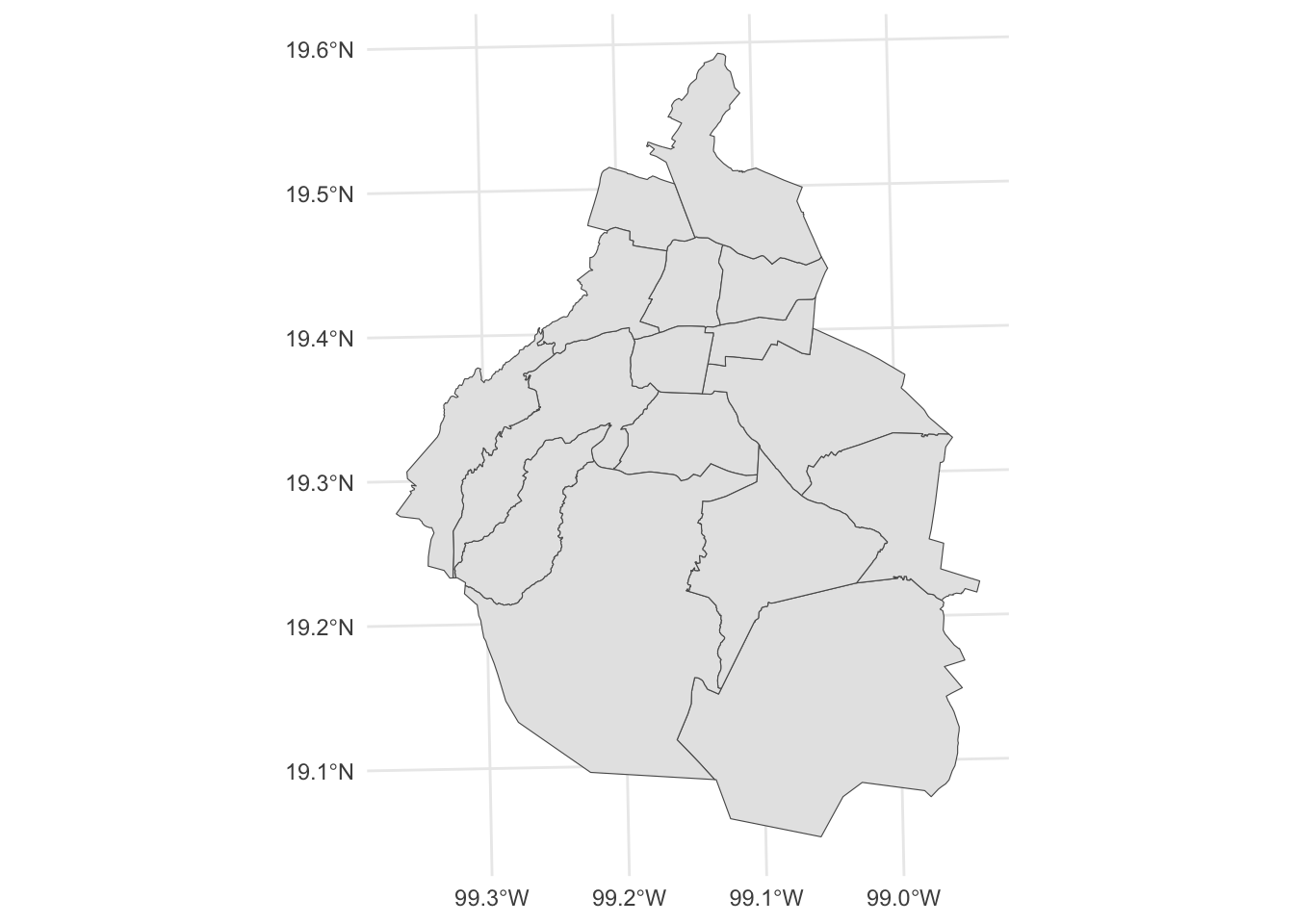

Podemos agregar los puntos dentro de la gráfica (ojo a veces los puntos y las gráficas utilizan diferentes proyecciones que hay que homologar)

ggplot(cdmx) +
  geom_sf(aes(geometry = geometry)) +
  geom_point(aes(x = longitud, y = latitud), data = df_robos) +
  theme_minimal()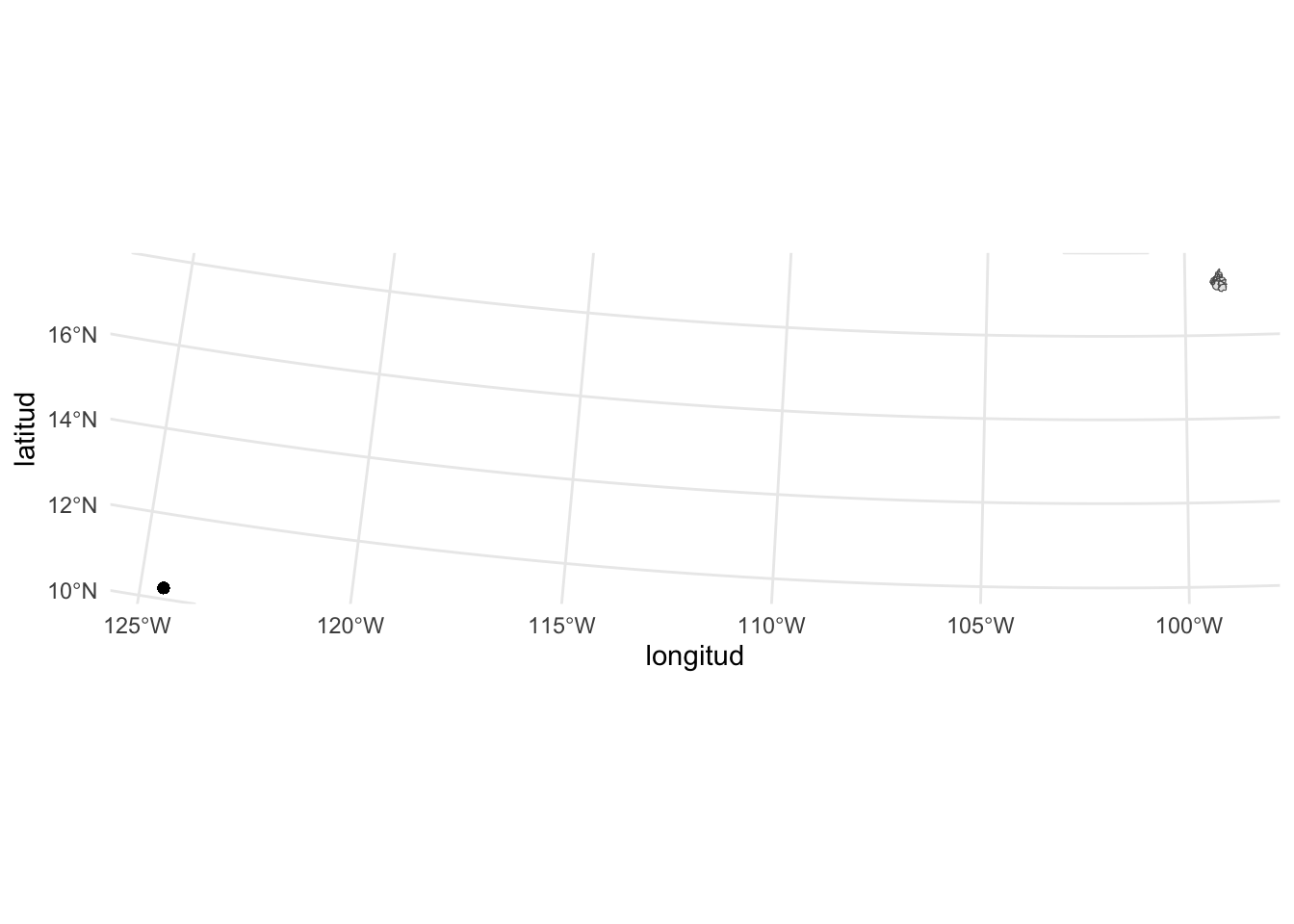

Notamos que algunos de los puntos caen lejos de nuestra unidad de análisis (CDMX) por lo que restringimos los puntos a caer dentro de uno de los polígonos de geom_sf

# Convertimos la latitud y longitud a un objeto `simple features` también
# el comando crs especifica el sistema de coordenadas usado (viene en el diccionario)
sf_robos <- df_robos |>
  st_as_sf(coords = c("longitud", "latitud"), crs = "WGS84")

# Homologamos los sistemas de coordenadas (el del INEGI tiene otro crs)
sf_robos <- sf_robos |> st_transform(st_crs(cdmx))

# Intersecamos los robos que ocurrieron en cdmx:
sf_robos <- sf_robos |> st_intersection(cdmx)

Ahora sí ya coinciden:

ggplot() +
  geom_sf(aes(geometry = geometry), data = cdmx) +
  geom_sf(aes(geometry = geometry), data = sf_robos) + #Ojo aquí cambia a geom_sf
  theme_minimal()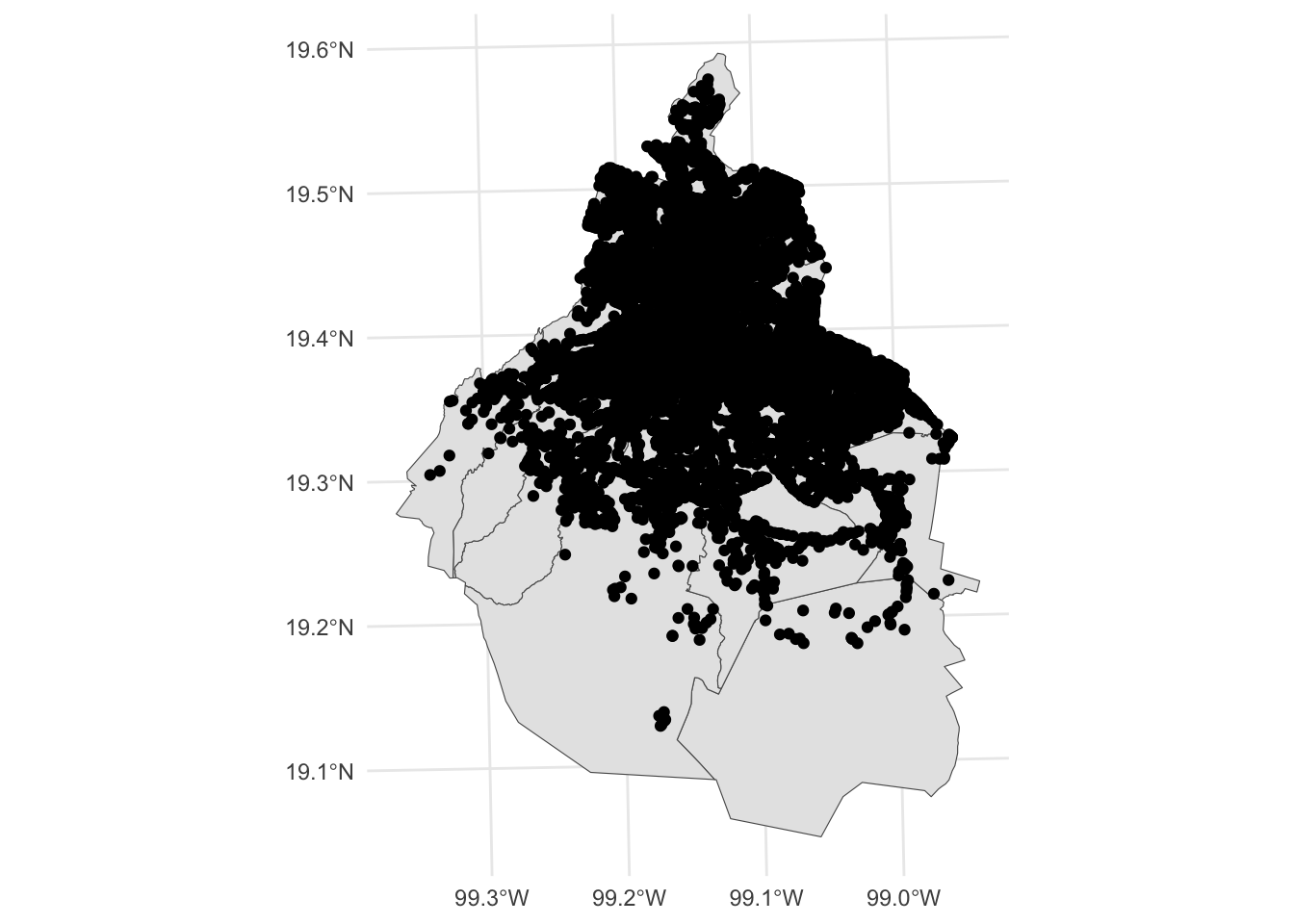

Densidad

Se puede ajustar una densidad kernel al proceso puntual. Ésta consiste en dividir el espacio \(\mathcal{B} \subset \mathbb{R}^2\) en ventanas (pixeles) del mismo tamaño (\(V_1, V_2, \dots, V_n\)) y calcular la cantidad de observaciones (\(N(V_1), N(V_2), \dots, N(V_n)\)) en cada uno de los sitios. La densidad conlleva además un proceso de suavizamiento adicional (el mismo que las densidades kernel de Wasserman (2006) pero bidimensionales) que se encuentra descrito en Ellis (1991).

Para construir la densidad hay que conertir el objeto sf en un objeto ppp (poisson point process) de la librería spatstat:

# Convertimos a proceso puntual (spatstat)
robos_point_process <- as.ppp(sf_robos$geometry, W = as.owin(cdmx))

# Calculamos la densidad de puntos del proceso
robos_densidad <- density(robos_point_process)

# Convertimos de vuelta a objeto sf (a través de pointprocess -> stars -> sf)
# https://www.andrewheiss.com/blog/2023/07/28/gradient-map-fills-r-sf
densidad_sf <- robos_densidad |> 
  st_as_stars() |> 
  st_as_sf() |> 
  st_set_crs(st_crs(cdmx)) #Para poner la proyección específica

#Arreglamos los bordes de los pixeles:
densidad_sf <- densidad_sf |> st_intersection(cdmx)

Finalmente graficamos:

ggplot() +
  geom_sf(aes(geometry = geometry, fill = v), color = NA, data = densidad_sf) + #Ojo aquí cambia a geom_sf
  geom_sf(aes(geometry = geometry), data = cdmx, fill = NA, color = "white", linewidth = 0.25) +
  scale_fill_gradientn(guide = "none", colours = wes_palette("Zissou1")) +
  theme_void() + 
  ggtitle("Densidad de robos a pasajeros")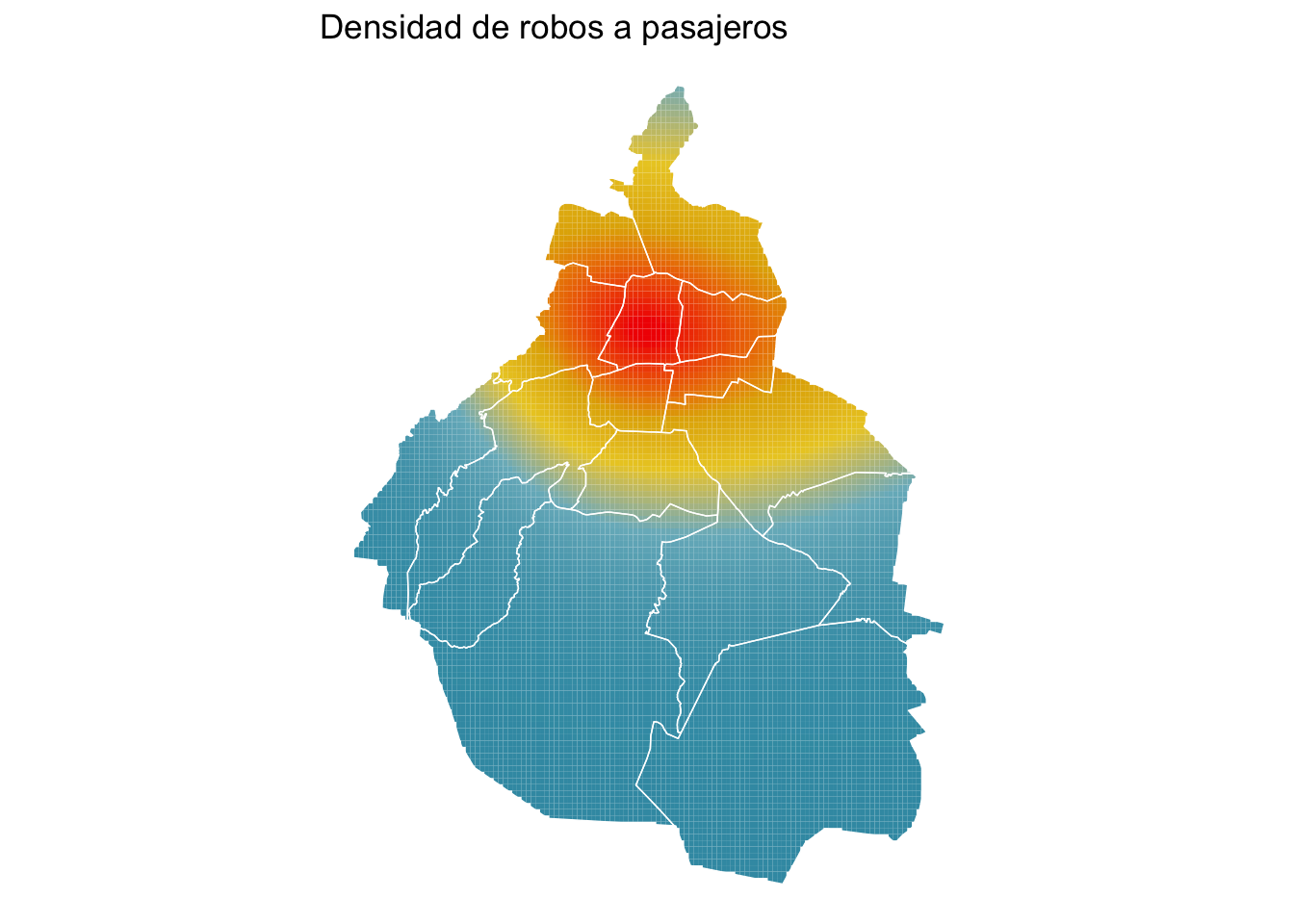

Tip

Por cierto que la referencia principal para procesos espaciales es Baddeley, Rubak, y Turner (2015).

Intensidades (de Papangelou)

La densidad no es la única medida espacial que puede generar mapas de calor. Otra medida de importancia es la intensidad. Todos los procesos de puntos, \(\mathcal{X} = \left\{X_1, X_2, \dots, X_k\right\}\), en el espacio son procesos puntuales. Para nuestros propósitos, la intensidad se define como una función \(\lambda(u, \mathcal{X})\) que depende del proceso (de los puntos en sí, \(\mathcal{X}\)) y de la posición en el espacio \(u\).

Nota

Podemos pensar la intensidad como el cambio infinitesimal en la probabilidad de ocurrencia de un evento en una bola de tamaño \(\delta\) centrada en \(u\) condicional al resto de los puntos:

\[ \lambda(u, \mathcal{X}) = \lim_{\delta \downarrow 0}\frac{\mathbb{P}(\text{Un evento ocurra en }B_{\delta}(u) | \text{El resto del proceso }\mathcal{X} \not\in B_{\delta(u)})}{\delta} \] En particular para los modelos que consideraremos, se supone que la intensidad tiene una forma paramétrica:

\[ \lambda(u, \mathcal{X}) = \exp\big(\theta^T B(u) + \gamma^{T} C(u, \mathcal{X})\big) \] donde \(\theta\) y \(\gamma\) son parámetros constantes, \(B(u)\) es una función de las coordenadas \(x\) y \(y\) y $ C(u, )$ es una función que depende tanto de las coordenadas como del resto del proceso. Al término \(B\) se le denomina tendencia espacial o trend y \(C\) se conocen como interacciones estocásticas o interactions. En los modelos de regresión, la forma específica de \(B\) y \(C\) se especifica eligiendo alguna familia paramétrica. Por ejemplo en los procesos Poisson no homogéneos: \[ \lambda(u, \mathcal{X}) = b(u) \]

o en los procesos Strauss:

\[ \lambda(u, \mathcal{X}) = \beta \gamma^{t_r(u,x)} \] donde \(t_r(u,x)\) es el número de puntos a una distancia \(r\) de \(u\).

Tip

En general se interpreta la intensidad como una tasa del número de eventos por unidad espacial.

En R podemos ajustar regresiones a los procesos puntuales mediante ppm para obtener la intensidad. En este caso, por ejemplo, ajusto un polinomio de segundo grado a las coordenadas x y y de mi proceso:

fit <- ppm(robos_point_process, trend = ~ polynom(x,y,2), Poisson())
intensidad <- predict(fit)

Sin embargo se pueden agregar otras covariables espaciales (por ejemplo altura ó fecha), así como cambiar la familia del proceso (ver por ejemplo Strauss() y otras ?pairwise.family).

Una vez estimada la intensidad se convierte de nuevo en un objeto sf y se grafica:

# Convertimos de vuelta a objeto sf (a través de pointprocess -> stars -> sf)
# https://www.andrewheiss.com/blog/2023/07/28/gradient-map-fills-r-sf
intensidad_sf <- intensidad |> 
  st_as_stars() |> 
  st_as_sf() |> 
  st_set_crs(st_crs(cdmx)) #Para poner la proyección específica

#Arreglamos los bordes de los pixeles:
intensidad_sf <- intensidad_sf |> st_intersection(cdmx)

ggplot() +
  geom_sf(aes(geometry = geometry, fill = v), color = NA, data = intensidad_sf) + #Ojo aquí cambia a geom_sf
  geom_sf(aes(geometry = geometry), data = cdmx, fill = NA, color = "white", linewidth = 0.25) +
  scale_fill_gradientn(guide = "none", colours = wes_palette("Zissou1")) +
  theme_void() +
  ggtitle("Intensidad de robos a pasajeros")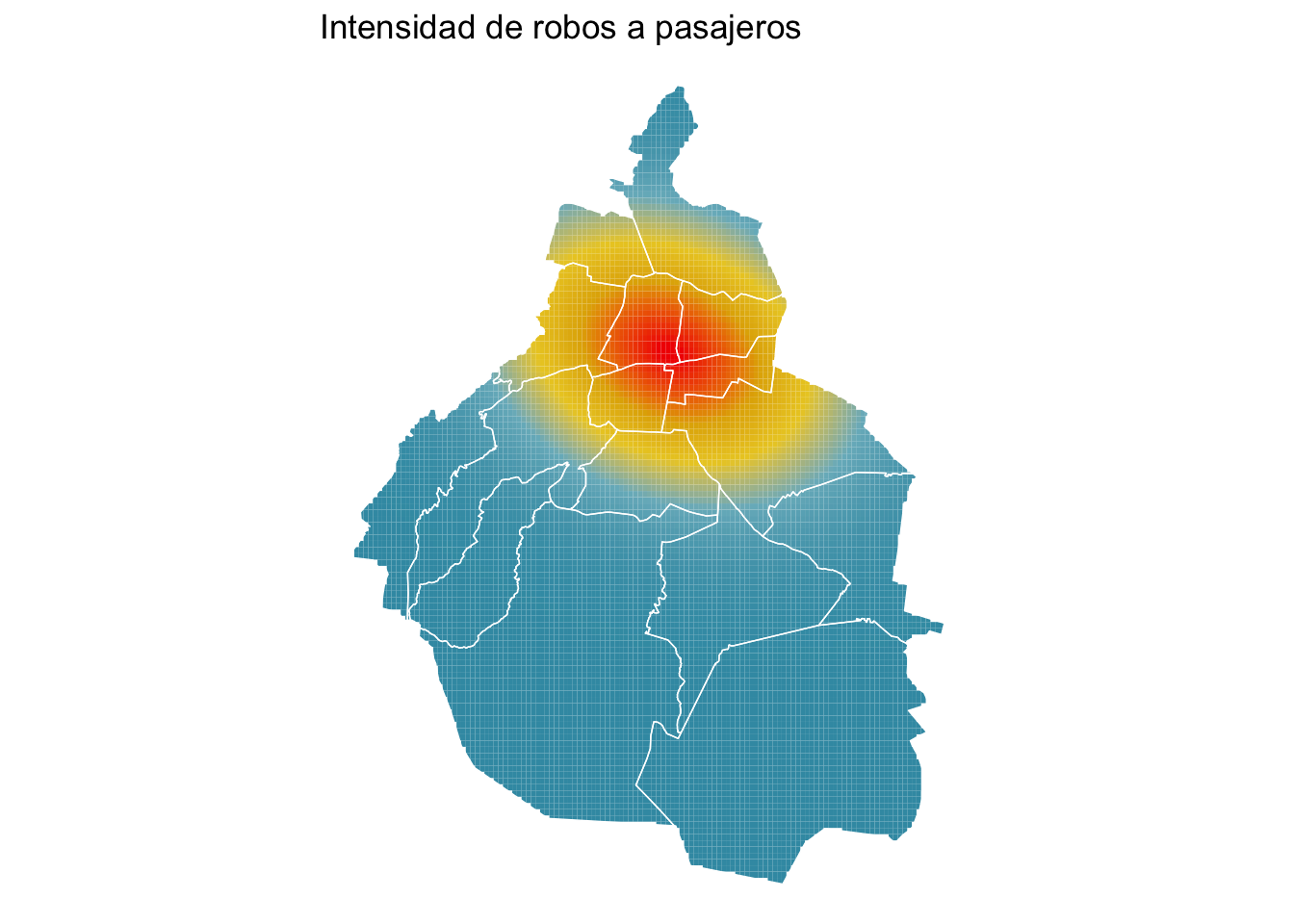

Despedida

Si en algún momento deseas un artículo de más profundidad sobre procesos puntuales espaciales ¡házmelo saber!

Referencias

Baddeley, Adrian, Ege Rubak, y Rolf Turner. 2015. Spatial point patterns: methodology and applications with R. CRC press.

Ellis, Steven P. 1991. «Density estimation for point processes». Stochastic processes and their applications 39 (2): 345-58.

Wasserman, Larry. 2006. All of nonparametric statistics. Springer Science & Business Media.